题目内容
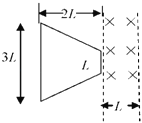
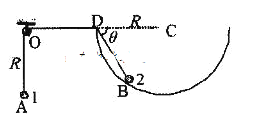
【题目】如图,可视为质点的小球1、2由不可伸长的细绳相连,小球1悬挂在定滑轮O的下方,小球2在半径为R的半球形固定容器内,定滑轮O与容器的边缘D及球心C在同一水平线上。系统静止时,小球1在定滑轮正下方R处的A点,小球2位于B点,BD间的细绳与水平方向的夹角θ=![]() 。已知小球1的质量为m,重力加速度为g,不计一切摩擦,忽略滑轮的质量。(结果用根号表示)
。已知小球1的质量为m,重力加速度为g,不计一切摩擦,忽略滑轮的质量。(结果用根号表示)
(1)试求小球2的质量;
(2)现将小球2置于D处由静止释放(小球1未触及地面),求小球1到达A点时的动能;
(3)在第(2)问中,小球2经过B点时,突然剪断细绳,求小球2经过容器晟低点时对容器的压力。
【答案】(1)小球2的质量![]() ;(2)小球1到达A点时的动能
;(2)小球1到达A点时的动能![]() ;(3)小球2对容器的压力大小也为
;(3)小球2对容器的压力大小也为![]() ,方向向下
,方向向下
【解析】
(1)设系统静止时细线中的拉力大小为T。小球受到容器的支持力![]() 方向沿BC。
方向沿BC。
由几何关系知![]() 为正三角形,所以
为正三角形,所以![]()
对小球1、小球2,根据共点力的平衡条件知
![]()
![]()
![]()
解得![]()
(2)设经过图示位置时小球1的速度为![]() ,小球2的速度为
,小球2的速度为![]() 。
。![]() 沿绳竖直向上,
沿绳竖直向上,![]() 沿圆弧切线斜向下。
沿圆弧切线斜向下。
由几何关系可知,![]() 与DB延长线的夹角为
与DB延长线的夹角为![]()
由运动关系可知,![]() 与
与![]() 应满足
应满足
![]()
由几何关系知 BD=R
根据机械能守恒定律,得
![]()
此时小球1的动能![]()
整理得![]()
(![]() ,
,![]() )
)
(3)细绳剪断后,小球2以![]() 为初速度,从B点沿圆弧运动到最低点,设经过最低点的速度为
为初速度,从B点沿圆弧运动到最低点,设经过最低点的速度为![]() ,根据机械能守恒定律,得:
,根据机械能守恒定律,得:![]()
设小球2经过容器最低点时受到的支持力为N。根据牛顿第二定律得:![]()
整理得:![]()
由牛顿第三定律知,小球2对容器的压力大小也为![]() 方向向下
方向向下

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目