题目内容
17.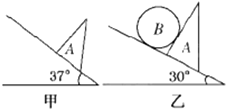 截面为直角三角形的木块A质量为M,放在倾角为θ的斜面上,当θ=37°时,木块恰能静止在斜面上.现将θ改为30°,在A与斜面间放一质量为m的光滑圆柱体B,如图乙,(sin37°=0.6,cos37°=0.8)则( )
截面为直角三角形的木块A质量为M,放在倾角为θ的斜面上,当θ=37°时,木块恰能静止在斜面上.现将θ改为30°,在A与斜面间放一质量为m的光滑圆柱体B,如图乙,(sin37°=0.6,cos37°=0.8)则( )| A. | A、B仍一定静止于斜面上 | |
| B. | 若M=2m,则A受到的摩擦力为$\frac{3}{2}$mg | |
| C. | 若M=8m,则A受到斜面的摩擦力为$\frac{9}{2}$mg | |
| D. | 以上说法都不对 |
分析 根据受力分析及平衡方程,来确定动摩擦因数与夹角的关系,从而求出动摩擦因数;当放在斜角为30°的斜面上,根据受力分析,结合力的平行四边形定则与滑动摩擦力的公式,即可求解.
解答 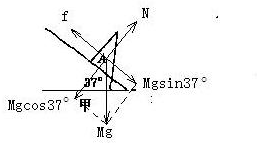 解:A、由题意可知,当θ=37°时,木块恰能静止在斜面上,则有:μMgcos37°=Mgsin37°;
解:A、由题意可知,当θ=37°时,木块恰能静止在斜面上,则有:μMgcos37°=Mgsin37°;
代入数据解得:μ=0.75.
现将θ改为30°,在A与斜面间放一质量为m的光滑圆柱体B,对A受力分析,
则有:f′=μN′
N′=Mgcos30°;
而F=mgsin30°
当f′<mgsin30°+Mgsin30°,则A相对斜面向下滑动,当f′>mgsin30°+Mgsin30°,则A相对斜面不滑动,因此A、B是否静止在斜面上,由B对A弹力决定,故A错误; 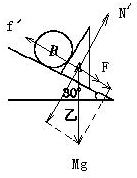
B、若M=2m,则mgsin30°+Mgsin30°=$\frac{3}{4}$Mg;
而f′=μN′=0.75×Mgcos30°=$\frac{3\sqrt{3}}{8}$Mg;
因f′<mgsin30°+Mgsin30°,A滑动,A受到斜面的滑动摩擦力,大小为f′=μN′=0.75×Mgcos30°=$\frac{3\sqrt{3}}{8}$Mg=$\frac{3\sqrt{3}}{4}$mg,故B错误;
C、若M=8m,则mgsin30°+Mgsin30°=$\frac{9}{16}$Mg;
而f′=μN′=0.75×Mgcos30°=$\frac{3\sqrt{3}}{8}$Mg;
因f′>mgsin30°+Mgsin30°,A不滑动,A受到斜面的静摩擦力,大小为:
mgsin30°+Mgsin30°=$\frac{9}{16}$Mg=$\frac{9}{2}$mg,故C正确,D错误;
故选:C
点评 考查对研究对象进行受力分析,掌握受力平衡方程,理解滑动摩擦力与静摩擦力的大小计算,注意会判定物体是否在斜面上滑动是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 我们说:“太阳东升西落”,是以地球为参考系的 | |
| B. | 我们说:“地球围绕太阳转”,是以地球为参考系的 | |
| C. | 诗中说:“卧看满天云不动”,是以云为参考系的 | |
| D. | 坐在火车上的乘客看到铁路旁的树木迎面向他飞奔而来,乘客是以火车为参考系的 |
| A. | 信号弹在夜空划出的痕迹就是信号弹运动的轨迹 | |
| B. | 画出信号弹的s-t图线,此图线就是信号弹的运动的轨迹 | |
| C. | 运动物体的s-t图线是曲线,则运动物体的轨迹也是曲线 | |
| D. | 匀速直线运动的位移-时间图象就是运动物体的轨迹 |
| A. | 匀变速直线运动是加速度不断增大的运动 | |
| B. | 匀变速直线运动是加速度不断减小的运动 | |
| C. | 匀变速直线运动是加速度保持不变的运动 | |
| D. | 匀变速直线运动是速度随位移均匀变化的运动 |
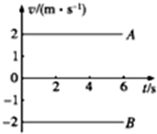
| A. | 质点A和B都是匀速直线运动,且它们的速度相同 | |
| B. | 在相同的时间内,质点A、B的位移大小相同 | |
| C. | 质点B在3秒内位移是6m | |
| D. | 质点A在第2秒内的位移是4m |
 我国“蛟龙号”深潜器曾经多次试验,终于在2012年6月24日以7020m深度成为世界上下潜最深的载人潜水器.假设在某次实验时,深潜器内的显示屏上显示出了从水面开始下潜到最后返回水面10min内速度图象,下列说法正确的是( )
我国“蛟龙号”深潜器曾经多次试验,终于在2012年6月24日以7020m深度成为世界上下潜最深的载人潜水器.假设在某次实验时,深潜器内的显示屏上显示出了从水面开始下潜到最后返回水面10min内速度图象,下列说法正确的是( )| A. | 本次下潜的最大深度为7020m | |
| B. | 全过程中最大加速度是0.025m/s2 | |
| C. | 0-4min内平均速度为1.5m/s | |
| D. | 0-1min和8-10min的时间内潜水员的速度和加速度方向均相反 |
| A. | 牛顿第一定律 | B. | 欧姆定律 | C. | 牛顿第二定律 | D. | 机械能守恒定律 |
| A. | 物体的位移大小是50 m,方向向北 | B. | 物体通过的路程是10 m | ||
| C. | 物体的位移大小是10 m,方向向北 | D. | 物体的位移大小是10 m,方向向南 |
| A. | 温度低的物体,内能不一定小 | |
| B. | 分子运动的平均速度可能为零,瞬时速度不可能为零 | |
| C. | 液体与大气相接触,表面层内分子所受其他分子的作用表现为相互吸引 | |
| D. | 0℃的铁和0℃的冰,它们的分子平均速率相同 | |
| E. | 气体分子单位时间内与单位面积器壁碰撞的次数与单位体积内的分子数和温度有关 |