题目内容
9.一小球以某一初速度由地面竖直向上运动,初动能为Ek,运动过程中受到空气阻力大小恒为重力的一半,上升的最大高度为H(落回地面后不反弹,以地面为零势能面).对于小球下列说法正确的是( )| A. | 小球落回地面时,小球的动能为$\frac{1}{3}$Ek | |
| B. | 小球运动到最高点时重力势能为$\frac{1}{2}$Ek | |
| C. | 小球上升高度为$\frac{H}{2}$时,小球重力势能等于小球动能 | |
| D. | 小球上升高度$\frac{H}{3}$过程中,小球损失的机械能为$\frac{1}{3}$Ek |
分析 空气阻力方向总是与物体速度方向相反,分析上升阶段与下降阶段的受力情况,根据牛顿第二定律分析加速度,判断速度如何变化.由运动学公式分析时间关系.
解答 解:A、上升过程:物体所受的空气阻力向下,与重力方向相同,根据动能定理得:-mgH-fH=0-Ek;所以:$H=\frac{{E}_{k}}{mg+f}=\frac{2{E}_{k}}{3mg}$;
下落过程:空气阻力向上与重力方向相反,根据动能定理得:mgH-fH=Ek′,联立得:${E}_{k}′=\frac{1}{3}{E}_{k}$.故A正确;
B、小球在最高点的重力势能:${E}_{Pm}=mgH=mg×\frac{2{E}_{k}}{3mg}=\frac{2}{3}{E}_{k}$.故B错误;
C、小球上升高度为$\frac{H}{2}$时,小球重力势能等于$\frac{1}{2}{E}_{m}$,即$\frac{1}{3}{E}_{K}$,根据动能定理${E}_{k}″-{E}_{k}=-(mg+f)•\frac{H}{2}$,小球的动能:${E}_{k}″=\frac{1}{2}{E}_{k}$.故C错误;
D、小球上升高度$\frac{H}{3}$过程中,小球损失的机械能等于阻力做的功,为:$△E=f•\frac{1}{3}H=\frac{1}{2}mg×\frac{1}{3}×\frac{2{E}_{k}}{3mg}=\frac{1}{9}{E}_{k}$,故D错误;
故选:A.
点评 本题借助于竖直上抛运动模型考查功能关系,要弄清空气阻力方向,运用动能定理与功能关系结合分析是关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
19.下列说法正确的是( )
| A. | 液晶的光学性质具有各向异性 | |
| B. | 空气的相对湿度定义为水的饱和蒸汽压与相同温度时空气中所含水蒸气的压强之比 | |
| C. | 小昆虫能在水面上自由走动与表面张力有关 | |
| D. | 玻璃、石墨和金刚石都是晶体,木炭是非晶体 |
20.下列几种情况下力F都对物体做了功:
①水平推力F推着质量为m的物体从静止开始在光滑水平面上前进了S;
②水平推力F推着质量为m的物体从静止开始在粗糙水平面上前进了S.
下列关于力F所做的功说法正确的是( )
①水平推力F推着质量为m的物体从静止开始在光滑水平面上前进了S;
②水平推力F推着质量为m的物体从静止开始在粗糙水平面上前进了S.
下列关于力F所做的功说法正确的是( )
| A. | ①做功最多 | B. | ②做功最多 | C. | 无法确定 | D. | 做功都相等 |
17.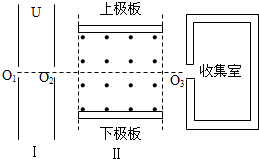 如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )
如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )
 如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )
如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )| A. | 区域Ⅱ的电场方向竖直向下 | |
| B. | 该装置可筛选出具有特定质量的粒子 | |
| C. | 该装置可筛选出具有特定速度的粒子 | |
| D. | 若射入的粒子电荷量相同,则该装置筛选出的粒子一定具有相同的质量 |
4.神舟六号载人航天飞船经过115小时32分钟的太空飞行,绕地球飞行77圈,飞船返回舱终于在2005年10月17日凌晨4时33分成功着陆,航天员费俊龙、聂海胜安全返回.已知万有引力常数G,地球表面的重力加速度g,地球的半径R,神舟六号飞船太空飞行近似为圆周运动.则下列论述正确的是( )
| A. | 可以计算神舟六号飞船绕地球的太空飞行离地球表面的高度 | |
| B. | 可以计算神舟六号飞船绕地球的太空飞行的加速度 | |
| C. | 飞船返回舱打开减速伞下降的过程中,飞船中的宇航员处于失重状态 | |
| D. | 飞船点火发射的过程中,飞船中的宇航员处于失重状态 |
18.用一根细绳连接物体与固定点,如果物体在光滑水平面上做匀速圆周运动时细绳突然断裂,下列说法正确的是( )
| A. | 物体将继续在原来的圆周上运动 | |
| B. | 物体将沿着圆周的切线方向飞出去 | |
| C. | 物体将沿着切线和圆周之间的某一条曲线向远离圆心的方向运动 | |
| D. | 物体将朝着圆心运动 |
19.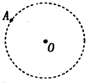 如图所示,A为太阳系中的天王星,它绕太阳O运行的轨道视为圆时,运动的轨道半径为R0,周期为T0.长期观测发现,天王星实际运动的轨道与圆轨道总有一些偏离,且每隔t0时间发生一次最大偏离,即轨道半径出现一次最大.根据万有引力定律,天文学家预言形成这种现象的原因可能是天王星外侧还存在着一颗未知的行星(假设其运动轨道与A在同一平面内,且与A的绕行方向相同),它对天王星的万有引力引起天王星轨道的偏离,由此可推测未知行星的运动轨道半径是( )
如图所示,A为太阳系中的天王星,它绕太阳O运行的轨道视为圆时,运动的轨道半径为R0,周期为T0.长期观测发现,天王星实际运动的轨道与圆轨道总有一些偏离,且每隔t0时间发生一次最大偏离,即轨道半径出现一次最大.根据万有引力定律,天文学家预言形成这种现象的原因可能是天王星外侧还存在着一颗未知的行星(假设其运动轨道与A在同一平面内,且与A的绕行方向相同),它对天王星的万有引力引起天王星轨道的偏离,由此可推测未知行星的运动轨道半径是( )
 如图所示,A为太阳系中的天王星,它绕太阳O运行的轨道视为圆时,运动的轨道半径为R0,周期为T0.长期观测发现,天王星实际运动的轨道与圆轨道总有一些偏离,且每隔t0时间发生一次最大偏离,即轨道半径出现一次最大.根据万有引力定律,天文学家预言形成这种现象的原因可能是天王星外侧还存在着一颗未知的行星(假设其运动轨道与A在同一平面内,且与A的绕行方向相同),它对天王星的万有引力引起天王星轨道的偏离,由此可推测未知行星的运动轨道半径是( )
如图所示,A为太阳系中的天王星,它绕太阳O运行的轨道视为圆时,运动的轨道半径为R0,周期为T0.长期观测发现,天王星实际运动的轨道与圆轨道总有一些偏离,且每隔t0时间发生一次最大偏离,即轨道半径出现一次最大.根据万有引力定律,天文学家预言形成这种现象的原因可能是天王星外侧还存在着一颗未知的行星(假设其运动轨道与A在同一平面内,且与A的绕行方向相同),它对天王星的万有引力引起天王星轨道的偏离,由此可推测未知行星的运动轨道半径是( )| A. | $\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$R0 | B. | R0$\sqrt{(\frac{{t}_{0}}{{t}_{0}-{T}_{0}})^{3}}$ | C. | R0$\root{3}{(\frac{{t}_{0}-{T}_{0}}{{t}_{0}})^{2}}$ | D. | R0$\root{3}{(\frac{{t}_{0}}{{t}_{0}-{T}_{0}})^{2}}$ |
 如图,一上端开口,下端封闭的细长玻璃管,下部有长l1=66cm的水银柱,中间封有长l2=6.5cm的空气柱,上部有长l3=56cm的水银柱,此时水银面恰好与管口平齐.已知大气压强为p0=76cmHg.如果使玻璃管绕底端在竖直平面内缓慢地转动一周,求在开口向下和转回到原来位置时管中空气柱的长度.封入的气体可视为理想气体,在转动过程中没有发生漏气.
如图,一上端开口,下端封闭的细长玻璃管,下部有长l1=66cm的水银柱,中间封有长l2=6.5cm的空气柱,上部有长l3=56cm的水银柱,此时水银面恰好与管口平齐.已知大气压强为p0=76cmHg.如果使玻璃管绕底端在竖直平面内缓慢地转动一周,求在开口向下和转回到原来位置时管中空气柱的长度.封入的气体可视为理想气体,在转动过程中没有发生漏气. 如图所示,两根水平的平行光滑长直金属导轨,其电阻不计,整个导轨处于竖直向下的匀强磁场中.导体棒ab和cd跨在导轨上,ab的电阻大于cd的电阻.当cd棒在水平外力F2作用下匀速向右滑动时,ab棒在水平外力F1作用下保持静止,则ab棒两端电压Uab和cd棒两端电压Ucd相比,Uab=Ucd,外力F1和F2相比,F1=F2.(均选填“>”、“=”或“<”)
如图所示,两根水平的平行光滑长直金属导轨,其电阻不计,整个导轨处于竖直向下的匀强磁场中.导体棒ab和cd跨在导轨上,ab的电阻大于cd的电阻.当cd棒在水平外力F2作用下匀速向右滑动时,ab棒在水平外力F1作用下保持静止,则ab棒两端电压Uab和cd棒两端电压Ucd相比,Uab=Ucd,外力F1和F2相比,F1=F2.(均选填“>”、“=”或“<”)