题目内容
11.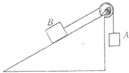 固定的光滑斜面倾角为37°,AB两个物块通过轻细绳连接跨过定滑轮,如图所示,开始时让物块B静止在斜面上,A离地面的高度h=0.1m,连接B物块的细绳与斜面平行,已知A的质量M=2kg,B的质量m=1kg,不计滑轮质量及细绳与滑轮间的摩擦,释放B物块后,B在A的带动下沿斜面上滑,A物块与地面碰撞后不反弹,斜面足够长,则( )
固定的光滑斜面倾角为37°,AB两个物块通过轻细绳连接跨过定滑轮,如图所示,开始时让物块B静止在斜面上,A离地面的高度h=0.1m,连接B物块的细绳与斜面平行,已知A的质量M=2kg,B的质量m=1kg,不计滑轮质量及细绳与滑轮间的摩擦,释放B物块后,B在A的带动下沿斜面上滑,A物块与地面碰撞后不反弹,斜面足够长,则( )| A. | B物块的最大速度为$\sqrt{\frac{14}{15}}$m/s | |
| B. | B物块的最大速度为$\sqrt{\frac{2}{3}}$m/s | |
| C. | B物块沿斜面上升的最大位移为$\frac{8}{45}m$ | |
| D. | B物块沿斜面上升的最大位移为$\frac{7}{45}m$ |
分析 A、B开始运动到A着地过程中,分析系统的受力及做功情况,系统的机械能守恒,运用机械能守恒定律求出它们的速度.
A着地后,B沿斜面做匀减速运动,当速度减为零时,B能沿斜面滑行的距离最大
解答 解:A、当物体A将要落地时,B的速度最大,由机械能守恒定律可知:
Mgh-mghsin37°=$\frac{1}{2}$(M+m)v2;
解得:v=$\sqrt{\frac{14}{15}}$m/s;故A正确,B错误;
C、A落地后,B继续上升,对上升过程由机械能守恒定律可得:
mgxsin37°=$\frac{1}{2}$mv12;
解得:x=$\frac{7}{90}$m;
故上升的总位移x=0.1+$\frac{7}{90}$=$\frac{8}{45}m$
故C正确,D错误;
故选:AC.
点评 本题要明确机械能守恒定律的应用,在A落地之前,A、B单个物体机械能不守恒,但二者组成的系统机械能守恒.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
1.关于下抛运动,下列说法中正确的是( )
| A. | 下抛运动是直线运动 | B. | 下抛运动是曲线运动 | ||
| C. | 下抛运动的初速度方向竖直向上 | D. | 质量大的物体下抛时速度增加得快 |
6.如图,一根轻弹簧两端固连物块a和b,质量分别为ma和mb放在水平的光滑桌面上.现同时施给它们方向如图所示的推力Fa和拉力Fb,发现二者运动过程中弹簧伸长了,则ma和mb满足的关系式为( )


| A. | maFb>mbFa | B. | maFb<mbFa | C. | maFa>mbFb | D. | maFa<mbFb |
16.下列关于时刻和时间的理解,下列说法正确的是( )
| A. | 时刻就是一瞬间,即一段很短的时间间隔 | |
| B. | 时间和时刻的本质是相同的,可以不加区别的利用 | |
| C. | 时间是指两个不同时刻之间的间隔 | |
| D. | 一段时间包含无数个时刻,所以把任意时刻都加到一起就是时间 |
 如图所示,某水银气压计的玻璃管顶端高出水银槽液面1m,因上部混入少量空气使读数不准,当气温为27℃时、标准气压计读数为76cmHg时,该气压计读数为70cmHg,求:
如图所示,某水银气压计的玻璃管顶端高出水银槽液面1m,因上部混入少量空气使读数不准,当气温为27℃时、标准气压计读数为76cmHg时,该气压计读数为70cmHg,求: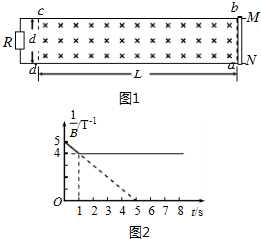 如图1所示,固定于绝缘水平面上且间距d=0.2m的U形金属框架处在竖直向下、均匀分布的磁场中,磁场的左边界cd与右边界ab之间的距离L=1m.t=0时,长为d的金属棒MN从ab处开始沿框架以初速度v0=0.2m/s向左运动,t=5s时棒刚好到达cd处停下;t=0时刻开始,磁场的磁感应强度B的倒数随时间t的变化规律如图2所示.电阻R=0.4Ω,棒的电阻r=0.1Ω,不计其他电阻和一切摩擦阻力,棒与导轨始终垂直且接触良好.求:
如图1所示,固定于绝缘水平面上且间距d=0.2m的U形金属框架处在竖直向下、均匀分布的磁场中,磁场的左边界cd与右边界ab之间的距离L=1m.t=0时,长为d的金属棒MN从ab处开始沿框架以初速度v0=0.2m/s向左运动,t=5s时棒刚好到达cd处停下;t=0时刻开始,磁场的磁感应强度B的倒数随时间t的变化规律如图2所示.电阻R=0.4Ω,棒的电阻r=0.1Ω,不计其他电阻和一切摩擦阻力,棒与导轨始终垂直且接触良好.求: 如图所示为自耦变压器,当它的滑键P向上移动、Q不动时,电压表读数将变小,电流表读数变小;若P不动,Q向上滑动时V示数将不变,A示数将变大(填“变大”、“变小”、“不变”)
如图所示为自耦变压器,当它的滑键P向上移动、Q不动时,电压表读数将变小,电流表读数变小;若P不动,Q向上滑动时V示数将不变,A示数将变大(填“变大”、“变小”、“不变”)