��Ŀ����
2��Сǿͬѧ���������õ��ڲ��������ٶȡ���ʵ��ʱ���Ȳ�ð��߳�ΪL������ֱ��ΪD��Ȼ���������¼�˵���n��ȫ�����õ�ʱ��Ϊt������1����ͬѧ�����������ٶȵı���ʽΪ��g=$\frac{4{��}^{2}{n}^{2}��L+r��}{{t}^{2}}$��
��2������ѡ����ͬѧ��õ�gֵƫС�����ܵ�ԭ����BC
A������߳�ʱ�������ù���
B�������϶�δ�ι̵�ϵ�����㣬���г����ɶ���ʹ���߳���������
C����ʼ��ʱʱ�������ǰ����
D��ʵ������49��ȫ����Ϊ50��
��3��Ϊ�����ʵ�龫�ȣ���ʵ���пɸı伸�ΰ��߳�L�������Ӧ������T���Ӷ��ó�һ���Ӧ��L��T�����ݣ�����LΪ�����꣮T2Ϊ�����꽫������������ֱ�ߣ�����ø�ֱ�ߵ�б��k�����������ٶ�g=$\frac{4{��}^{2}}{K}$����k��ʾ�������ִ���ʵ�����ݵķ����õ���gֵ������ֵ�����ȣ��ƫ��ƫС������ȡ�����
���� ��1��������ڰڳ������ڣ�Ȼ���ɵ��ڵ����ڹ�ʽ����������ٶȵı���ʽ��
��2�������������ٶȵı���ʽ�������������ٶȲ���ֵƫС��ԭ��
��3�����ݵ��ڵ����ڹ�ʽ�ó��������ٶ�g�ı���ʽ���Ӷ��жϳ�gֵ����ƫ���ԭ��
��� �⣺��1�����ڰڳ�l=L+r����������T=$\frac{t}{n}$��
�ɵ������ڹ�ʽT=2��$\sqrt{\frac{l}{g}}$�ɵã�g=$\frac{4{��}^{2}l}{{T}^{2}}$=$\frac{4{��}^{2}{n}^{2}��L+r��}{{t}^{2}}$
��2��A������߳�ʱ�������ù��������ڰڳ�ƫ��l����g=$\frac{4{��}^{2}l}{{T}^{2}}$��֪��
�������ٶȵIJ���ֵƫ���������⣬��A����
B�������϶�δ�ι̵�ϵ�����㣬���г����ɶ���ʹ���߳��������ˣ�
����ʱ��������ֵ���㣬lƫС����g=��֪���������ٶȵIJ���ֵƫС���������⣬��B��ȷ��
C����ʼ��ʱ��������簴�£�����ʱ��tƫ����g=$\frac{4{��}^{2}l}{{T}^{2}}$=$\frac{4{��}^{2}{n}^{2}��L+r��}{{t}^{2}}$��֪��
�������ٶȵIJ���ֵƫ�������⣬��C��ȷ��
D��ʵ������49��ȫ����Ϊ50�Σ�Nƫ����g=$\frac{4{��}^{2}{n}^{2}��L+r��}{{t}^{2}}$��֪��
�������ٶȲ���ֵƫ���������⣬��D����
��ѡ��BC
��3����lΪ�����ꡢT2Ϊ�����꽫������������ֱ�ߣ�����ø�ֱ�ߵ�б��K���پݵ��ڵ����ڹ�ʽT=2��$\sqrt{\frac{l}{g}}$�ã�g=$\frac{4{��}^{2}l}{{T}^{2}}$������g=$\frac{4{��}^{2}}{K}$
�ʴ�Ϊ����1��$\frac{{4{��^2}{n^2}��L+\frac{D}{2}��}}{t^2}$��2��BC ��3��$\frac{{4{��^2}}}{K}$���
���� ����ؼ�Ҫ����ʵ���ԭ�������ڵ����ڹ�ʽT=2��$\sqrt{\frac{l}{g}}$ Ҫ�ܸ���ʵ��ԭ��������ʵ����

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д��ټ��ٶ���ͬ �����ʱ���ٶ���ͬ �����е�ʱ����� �����ʱ�Ķ�����ȣ�
| A�� | �٢� | B�� | �ڢ� | C�� | �٢� | D�� | �ڢ� |
| A�� | ��ľ��ʼ����ʱ�����ҵĽ��ٶȽϴ������ж� | |
| B�� | ��ľ��ʼ����ʱ�����ҵ����ٶȽϴ������ж� | |
| C�� | ��ľ��ʼ����ʱ�����ҵ����ļ��ٶȽ�С�������ж� | |
| D�� | ��ľ���˵ľ���ȱ����ѧ���� |
| A�� | ���������ǹ��ƫ������ | |
| B�� | ���㲣�������ڵ���Ʒʱ�������ھ�ͷǰ��װһ��ƫ��Ƭ����������ǿ�� | |
| C�� | ���ά�������ź������˹��ȫ����ԭ�� | |
| D�� | ��������������ҫ�³��ֳ���ɫ�������ǹ���������� |
 �̶��Ĺ⻬б�����Ϊ37�㣬AB�������ͨ����ϸ�����ӿ�������֣���ͼ��ʾ����ʼʱ�����B��ֹ��б���ϣ�A�����ĸ߶�h=0.1m������B����ϸ����б��ƽ�У���֪A������M=2kg��B������m=1kg�����ƻ���������ϸ���뻬�ּ��Ħ�����ͷ�B����B��A�Ĵ�������б���ϻ���A����������ײ������б���㹻����������
�̶��Ĺ⻬б�����Ϊ37�㣬AB�������ͨ����ϸ�����ӿ�������֣���ͼ��ʾ����ʼʱ�����B��ֹ��б���ϣ�A�����ĸ߶�h=0.1m������B����ϸ����б��ƽ�У���֪A������M=2kg��B������m=1kg�����ƻ���������ϸ���뻬�ּ��Ħ�����ͷ�B����B��A�Ĵ�������б���ϻ���A����������ײ������б���㹻����������| A�� | B��������ٶ�Ϊ$\sqrt{\frac{14}{15}}$m/s | |
| B�� | B��������ٶ�Ϊ$\sqrt{\frac{2}{3}}$m/s | |
| C�� | B�����б�����������λ��Ϊ$\frac{8}{45}m$ | |
| D�� | B�����б�����������λ��Ϊ$\frac{7}{45}m$ |
| A�� | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{r}{R}$ | B�� | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{R}^{2}}{{r}^{2}}$ | C�� | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{r}{R}$ | D�� | $\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{R}{r}}$ |
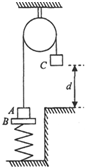 ��ͼ��ʾ������ϵ��Ϊk�����ʵ����¶˹̶����϶���B�������ӣ�����A������B�ϣ�A��C������ͨ��ϸ�����Ӳ�����ڹ⻬�Ļ����ϣ���ʼʱ����Cʹ֮��ֹ�������Ӹպ���ֱ��δ��������֪A��B��C�����ֱ�Ϊm��2m��2m��C���Ҳ�ƽ̨�ĸ߶Ȳ�Ϊd����C�ɾ�ֹ�ͷź�C�����˶�ͬʱ����A��B��������֪��A��B����֮ǰC��δ�䵽ƽ̨�ϣ���ȫ����A���岻���������֣����Կ�������Ӱ�죬�������ٶ�Ϊg����֪���ɵ�������E�����α�����x֮��Ĺ�ϵ����E��=$\frac{1}{2}$k��x2���������ͷ�C����˶������У�
��ͼ��ʾ������ϵ��Ϊk�����ʵ����¶˹̶����϶���B�������ӣ�����A������B�ϣ�A��C������ͨ��ϸ�����Ӳ�����ڹ⻬�Ļ����ϣ���ʼʱ����Cʹ֮��ֹ�������Ӹպ���ֱ��δ��������֪A��B��C�����ֱ�Ϊm��2m��2m��C���Ҳ�ƽ̨�ĸ߶Ȳ�Ϊd����C�ɾ�ֹ�ͷź�C�����˶�ͬʱ����A��B��������֪��A��B����֮ǰC��δ�䵽ƽ̨�ϣ���ȫ����A���岻���������֣����Կ�������Ӱ�죬�������ٶ�Ϊg����֪���ɵ�������E�����α�����x֮��Ĺ�ϵ����E��=$\frac{1}{2}$k��x2���������ͷ�C����˶������У�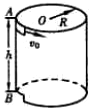 ��ֱԲͲ�ڱڹ⻬���뾶ΪR�����������A����A�����·�h���г���B��һ����Ϊm��С������A��ԲͲ�ڱ����߷���ˮƽ����ԲͲ�ڣ�Ҫʹ���B���ɳ������ƿ�����������
��ֱԲͲ�ڱڹ⻬���뾶ΪR�����������A����A�����·�h���г���B��һ����Ϊm��С������A��ԲͲ�ڱ����߷���ˮƽ����ԲͲ�ڣ�Ҫʹ���B���ɳ������ƿ�����������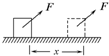 ��ͼ��ʾ������Ϊ2kg��������ˮƽ�����ϣ��ܵ���ˮƽ�����37��ǡ���СΪ10N���������ã��ƶ�2m����֪�����������Ķ�Ħ��������=0.2����
��ͼ��ʾ������Ϊ2kg��������ˮƽ�����ϣ��ܵ���ˮƽ�����37��ǡ���СΪ10N���������ã��ƶ�2m����֪�����������Ķ�Ħ��������=0.2����