��Ŀ����
5�� ��ͼ1��ʾ���̶��ھ�Եˮƽ�����Ҽ��d=0.2m��U�ν�����ܴ�����ֱ���¡����ȷֲ��Ĵų��У��ų�����߽�cd���ұ߽�ab֮��ľ���L=1m��t=0ʱ����Ϊd�Ľ�����MN��ab����ʼ�ؿ���Գ��ٶ�v0=0.2m/s�����˶���t=5sʱ���պõ���cd��ͣ�£�t=0ʱ�̿�ʼ���ų��ĴŸ�Ӧǿ��B�ĵ�����ʱ��t�ı仯������ͼ2��ʾ������R=0.4�������ĵ���r=0.1�����������������һ��Ħ�����������뵼��ʼ�մ�ֱ�ҽӴ����ã���
��ͼ1��ʾ���̶��ھ�Եˮƽ�����Ҽ��d=0.2m��U�ν�����ܴ�����ֱ���¡����ȷֲ��Ĵų��У��ų�����߽�cd���ұ߽�ab֮��ľ���L=1m��t=0ʱ����Ϊd�Ľ�����MN��ab����ʼ�ؿ���Գ��ٶ�v0=0.2m/s�����˶���t=5sʱ���պõ���cd��ͣ�£�t=0ʱ�̿�ʼ���ų��ĴŸ�Ӧǿ��B�ĵ�����ʱ��t�ı仯������ͼ2��ʾ������R=0.4�������ĵ���r=0.1�����������������һ��Ħ�����������뵼��ʼ�մ�ֱ�ҽӴ����ã�����1����0��1s�ڰ��ܵ��İ�������
��2����������m��
��3����0��5s�ڵ���R���ĵ�ƽ���繦��P1��
���� ��1����t=0ʱ�̿�ʼ���ų��ĴŸ�Ӧǿ��B�ĵ�����ʱ��t�ı仯���ɣ�˵����·��û�и�Ӧ������������ͨ�����䣬�ݴ���ʽ����֪��1s�ڵ���������˶����Ӷ�������⣮
��2��B���ֲ��������������˶����ɶ���������ʽ����ϵ��������Ĺ�ϵ��������������
��3�����������غ�õ���·�����Ľ����ȣ���Ϊ�繦�Ĵ�С������ƽ���繦��P��
��� �⣺��1����t=0ʱ�̿�ʼ���ų��ĴŸ�Ӧǿ��B�ĵ�����ʱ��t�ı仯���ɣ�
��$\frac{1}{B}=5-t$��
��0.2��1=B��1-0.2t��
����B0Ld=B��L-v0t��d����
˵����·��û�и�Ӧ������������ͨ�����䣬��˵���������˶���
��ô��0��1s�ڰ��ܵ��İ�����Ϊ�㣻
��2��t=1sʱB=0.25T����1s��λ��Ϊ��x=v0t=0.2m����
�ӵ�1sĩ����5sĩ��������������˶���ȡ����Ϊ�������ݶ��������ã�
-B$\overline{I}$d•t=0-mv0����
��$\overline{I}$t=q=$\frac{\overline{E}t}{R+r}$=$\frac{Bd\overline{v}t}{R+r}$=$\frac{Bd��L-x��}{R+r}$=$\frac{0.25��0.2����1-0.2��}{0.4+0.1}$=0.08C����
���ɢܵã�m=$\frac{Bqd}{{v}_{0}}$=$\frac{0.25��0.08��0.2}{0.2}$kg=0.02kg
��3��0-5s�ڻ�·�������ܽ�����Ϊ��Q=$\frac{1}{2}$m${v}_{0}^{2}$=4��10-4J
����R�����Ľ�����Ϊ��QR=$\frac{R}{R+r}$Q=3.2��10-4J
�����R�ϵ繦Ϊ��W=QR=3.2��10-4J
0-5s�ڵ���R���ĵ�ƽ���繦��Ϊ��P=$\frac{W}{t}$=$\frac{3.2��1{0}^{-4}}{5}$=6.4��10-5W
�𣺣�1����1s�ڣ����ܵ��İ�����Ϊ�㣻
��2����������Ϊ0.02kg��
��3��0-5s�ڵ���R���ĵ�ƽ���繦��Ϊ6.4��10-5W��
���� �������ؼ����յ���·��û�и�Ӧ��������ʱ����·�ܵĴ�ͨ��Ӧ���ֲ��䣮���ö������������q����Ӧ��������ʽΪq=$\frac{����}{R+r}$���dz��õ�˼·��Ҫ��ǿ�ⷽ�����ϰ����߽���������

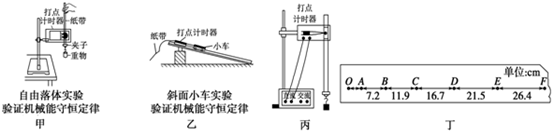
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | ��ľ��ʼ����ʱ�����ҵĽ��ٶȽϴ������ж� | |
| B�� | ��ľ��ʼ����ʱ�����ҵ����ٶȽϴ������ж� | |
| C�� | ��ľ��ʼ����ʱ�����ҵ����ļ��ٶȽ�С�������ж� | |
| D�� | ��ľ���˵ľ���ȱ����ѧ���� |
 �̶��Ĺ⻬б�����Ϊ37�㣬AB�������ͨ����ϸ�����ӿ�������֣���ͼ��ʾ����ʼʱ�����B��ֹ��б���ϣ�A�����ĸ߶�h=0.1m������B����ϸ����б��ƽ�У���֪A������M=2kg��B������m=1kg�����ƻ���������ϸ���뻬�ּ��Ħ�����ͷ�B����B��A�Ĵ�������б���ϻ���A����������ײ������б���㹻����������
�̶��Ĺ⻬б�����Ϊ37�㣬AB�������ͨ����ϸ�����ӿ�������֣���ͼ��ʾ����ʼʱ�����B��ֹ��б���ϣ�A�����ĸ߶�h=0.1m������B����ϸ����б��ƽ�У���֪A������M=2kg��B������m=1kg�����ƻ���������ϸ���뻬�ּ��Ħ�����ͷ�B����B��A�Ĵ�������б���ϻ���A����������ײ������б���㹻����������| A�� | B��������ٶ�Ϊ$\sqrt{\frac{14}{15}}$m/s | |
| B�� | B��������ٶ�Ϊ$\sqrt{\frac{2}{3}}$m/s | |
| C�� | B�����б�����������λ��Ϊ$\frac{8}{45}m$ | |
| D�� | B�����б�����������λ��Ϊ$\frac{7}{45}m$ |
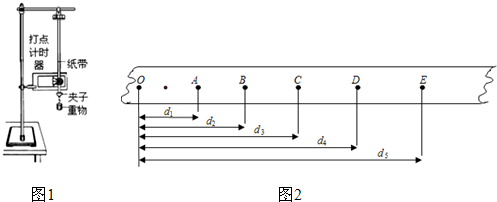
 ������������ӣ�������������OC����ͬʱ��O������ų�������˵����ȷ���ǣ�������
������������ӣ�������������OC����ͬʱ��O������ų�������˵����ȷ���ǣ�������| A�� | ����һ�����Ӵ�OA������ų�������һ������һ����OB������ų� | |
| B�� | ����һ�����Ӵ�OB������ų�������һ������һ����CA������ų� | |
| C�� | ���������ӷֱ��A��B��������ų����������ڴų����˶���ʱ��֮��Ϊ2��1 | |
| D�� | ���������ӷֱ��A��B��������ų����������ڴų����˶��Ĺ���뾶֮��Ϊ1��$\sqrt{3}$ |
| A�� | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{r}{R}$ | B�� | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{R}^{2}}{{r}^{2}}$ | C�� | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{r}{R}$ | D�� | $\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{R}{r}}$ |
 ��ͼ��ʾ������Ϊm�Ļ�����ˮƽ����������vײ�Ͼ���ϵ��Ϊk�����ʵ��ɣ������齫����ѹ����x0ʱ�ٶȼ�С���㣬Ȼ���ֽ����������ƿ�����֪������ˮƽ���Ķ�Ħ������Ϊ�̣��������̵���δ�����������Ҷ���δ˩�ӣ��������ж���ȷ���ǣ�������
��ͼ��ʾ������Ϊm�Ļ�����ˮƽ����������vײ�Ͼ���ϵ��Ϊk�����ʵ��ɣ������齫����ѹ����x0ʱ�ٶȼ�С���㣬Ȼ���ֽ����������ƿ�����֪������ˮƽ���Ķ�Ħ������Ϊ�̣��������̵���δ�����������Ҷ���δ˩�ӣ��������ж���ȷ���ǣ�������| A�� | ���������˶������У������е����������С | |
| B�� | �����뵯�ɽӴ������У�����Ļ�е���ȼ�С������ | |
| C�� | ������ͣ�ھ��뵯���Ҷ�$\frac{{v}^{2}}{2��g}$-2x0�� | |
| D�� | �����뵯�ɽӴ������У������뵯����ɵ�ϵͳ��е��һֱ��С |
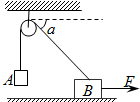 ��ͼ��ʾ������A��B��������Ϊm���ҷֱ����������ֵ��������ӣ��������뻬�֡���������֮���Ħ����������ˮƽ����F������B��ˮƽ����������2m/s���ٶ�������ֱ���˶��Ĺ����У����ӵ�����������A���������������=����������������=60��ʱ��������A���ٶȴ�С1m/s��
��ͼ��ʾ������A��B��������Ϊm���ҷֱ����������ֵ��������ӣ��������뻬�֡���������֮���Ħ����������ˮƽ����F������B��ˮƽ����������2m/s���ٶ�������ֱ���˶��Ĺ����У����ӵ�����������A���������������=����������������=60��ʱ��������A���ٶȴ�С1m/s��