题目内容
【题目】如图所示,粗细均匀的圆木棒A下端离地面高h,上端套着一个细环B.A和B的质量均为m,A和B间的滑动摩擦力为f,且f<mg.用手控制A和B,使它们从静止开始自由下落,当A与地面碰撞后,A以碰撞地面时的速度大小竖直向上运动,与地面碰撞时间极短,空气阻力不计,运动过程中A始终呈竖直状态.求:
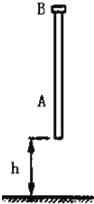
(1)木棒A与地面第一次碰撞后A、B的加速度大小和方向;
(2)若A再次着地前B不脱离A,A的长度应满足什么条件?
【答案】(1)A的加速度大小为![]() ,方向竖直向下;B的加速度大小为
,方向竖直向下;B的加速度大小为![]() ,方向竖直向下;
,方向竖直向下;
(2)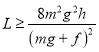
【解析】(1)木棒与环一起自由下落,设木棒着地时的速度为v0,则有v02=2gh
得: ![]()
木棒A与地面第一次碰撞后,木棒弹起竖直上升过程中,根据牛顿第二定律得
对木棒:f+mg=ma1
得 ![]() 方向竖直向下
方向竖直向下
对环:mg-f=ma2
得![]() 方向竖直向下
方向竖直向下
(2)环在木棒上升及下降的全过程中一直处于向下加速运动状态,木棒从向上弹起到再次着地的过程中木棒与环的加速度均保持不变.
木棒在空中运动的时间为![]()
在这段时间内,环运动的位移为![]()
要使环不碰地面,则要求木棒长度不小于x,即L≥x
解得: 

练习册系列答案
相关题目