题目内容
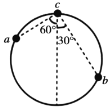
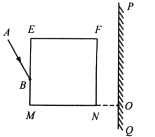
【题目】回旋加速器核心部分是两个D形金属扁盒，两盒分别和一高频交流电源两极相接．以便在盒间的窄缝中形成匀强电场，使粒子每次穿过狭缝都得到加速．两盒放在磁惑应强度为B的匀强磁场中．磁场方向垂直于盒底面．粒子源置于盒的圆心附近，若粒子源射出的粒子带电荷量为q，质量为m，粒子最大回旋半径为Rn，其运动轨迹如图所示．问.
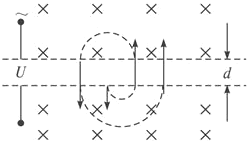
(1)D形盒内有无电场？
(2)粒子在盒内做何种运动？
(3)所加交流电压频率应是多大．粒子运动的角速度为多大？
(4)粒子离开加速器时速度为多大？最大动能为多少？
(5)设两D形盒间电场的电势差为U，盒间距离为d，其间电场均匀，求把静止粒子加速到上述能量所需时间．
【答案】(1) D形盒内无电场 (2) 粒子在盒内做匀速圆周运动 (3) 
， 
(4) 
，
(5) 
【解析】
(1)加速器由D形盒盒间缝隙组成，盒间缝隙对粒子加速，D形盒起到让粒子旋转再次通过盒间缝隙进行加速，要做匀速圆周运动，则没有电场．电场只存在于两盒之间，而盒内无电场.
(2)粒子在磁场中只受洛伦兹力作用，洛伦兹力始终与速度垂直，粒子做匀速圆周运动
(3)所加交流电压频率等于粒子在磁场中的频率，根据
和
可得
，
故频率
运动的角速度
(4)粒子速度增加则半径增加，当轨道半径达到最大半径时速度最大，由
得：
则其最大动能为：
(5)由能量守恒得：
则离子匀速圆周运动总时间为：
离子在匀强电场中的加速度为：
匀加速总时间为：
解得：
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
