题目内容
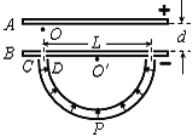
【题目】如图，两根足够长且平行的金属杆制成光滑金属导轨，导轨平面与水平面成α角，导轨宽为L，电阻忽略不计。空间有一足够大、与导轨所在平面垂直的匀强磁场。开始时导轨顶端接一不计内阻的稳压电源，电动势为E，如图A．所示。导体棒P垂直于导轨放置并始终与导轨接触良好，P的质量为m、电阻为R。
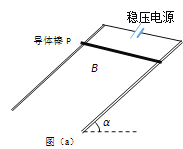
（1）释放P，它恰能静止在导轨上，求匀强磁场的磁感应强度的大小与方向；
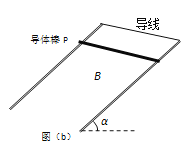
（2）若去掉稳压电源，用一根不计电阻的导线连接两根导轨的顶端，如图B．。再次由静止释放导体棒P。请通过分析，从速度、加速度的角度描述导体棒的运动；
（3）设导轨顶端接稳压电源时，通过静止导体棒的电流为I1；顶端接导线时，导体棒运动时其中的电流会无限逼近I2。请讨论I1、I2的大小分别由哪些因素决定。
【答案】（1）
，垂直于斜面向下（2）见解析（3）导体棒的质量m、斜面倾角α、磁感应强度B和轨道宽度L共同决定
【解析】
（1）根据闭合电路欧姆定律有：I=E/R
P静止在光滑的导轨上，受到重力、斜面弹力和安培力作用，其中安培力与重力沿斜面方向的分力为一对平衡力。有： mgsinα=F安=BIL
由以上二式可得：
根据左手定则，可以判定匀强磁场的磁感应强度的方向为垂直于斜面向下。
（2）用导线替换电源，静止释放P的瞬间，P仅受到重力和垂直斜面的弹力作用，从静止开始沿斜面向下做加速运动，初始加速度a0= gsinα。
运动后导体棒内产生感应电动势：E感= BIv
感应电流：
因此P受到安培力FA=BIL。根据牛顿第二定律有： ma= mgsinα- BIL
可得P的加速度a=gsinα
随着速度增大，加速度逐渐减小最后趋近于零，速度趋近于
所以，导体棒做加速度减小的加速度运动；加速度的大小从gsinα开始减小，最后趋近于零；速度的大小从0开始逐渐增大，最后趋近于
（3）I1是由稳恒电源在闭合回路中产生的电流，I1=E/R，所以它的大小由稳恒电源的电动势E和电路中的总电阻R决定。
导体棒切割磁感线产生感应电动势在闭合回路中产生的电流，
当速度v趋近于时，导体棒中的电流趋近于
，所以I2的大小由导体棒的质量m、斜面倾角α、磁感应强度B和轨道宽度L共同决定。
