题目内容
2.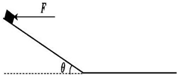 在倾角θ=37°的粗糙斜面上距离斜面底端s=1m处有一质量m=1kg的物块,受如图所示的水平恒力F的作用.物块由静止开始沿斜面下滑,到达底端时即撤去水平恒力F,物块在水平面上滑动一段距离后停止.已知物块与各接触面之间的动摩擦因数均为μ=0.2,g=10m/s2,sin 37°=0.6,cos 37°=0.8.
在倾角θ=37°的粗糙斜面上距离斜面底端s=1m处有一质量m=1kg的物块,受如图所示的水平恒力F的作用.物块由静止开始沿斜面下滑,到达底端时即撤去水平恒力F,物块在水平面上滑动一段距离后停止.已知物块与各接触面之间的动摩擦因数均为μ=0.2,g=10m/s2,sin 37°=0.6,cos 37°=0.8.(1)若物块在运动过程中的最大速度为2m/s,则水平恒力 F的大小为多少?
(2)若改变水平恒力F的大小,可使物块总的运动时间最短,则最短时间为多少?
分析 (1)物体在斜面上到达斜面底端时的速度最大为2m/s,由运动学公式求出加速度,由牛顿第二定律求的力F;
(2)利用运动学公式求出在斜面上和在水平面上的时间,由数学知识求的最小时间.
解答 解:(1)物块到达斜面底端时速度最大,
由匀变速直线运动的速度位移公式得:
v2=2as,解得,加速度:a=2m/s2,
物块在斜面上运动过程,由牛顿第二定律得:
mgsin θ-Fcos θ-μ(mgcos θ+Fsin θ)=ma,解得:F=2.6N.
(2)设物块在斜面上的加速度为a,运动时间为t1,在水平面上的运动时间为t2,
由匀变速直线运动的位移公式得:s=$\frac{1}{2}$at12,
到达底端时的速度:v=$\sqrt{2as}$=μgt2,
运动的总时间:t=t1+t2=$\sqrt{\frac{2s}{a}}$+$\frac{\sqrt{2as}}{μg}$
根据基本不等式,当a=μg=2m/s2时,t有最小值:tmin=2s.
答:(1)若物块在运动过程中的最大速度为2m/s,则水平恒力 F的大小为2.6N;
(2)若改变水平恒力F的大小,可使物块总的运动时间最短,则最短时间为2s.
点评 解决本题的关键能够正确地受力分析,运用牛顿第二定律和运动学公式以及动能定理求解,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
相关题目
12.一质量为1kg的物体从静止开始匀加速竖直下落,经2s落地,落地时速度大小为18m/s,若重力加速度g取10m/s2,则( )
| A. | 物体的重力势能减少了200J | B. | 物体的机械能减少了20J | ||
| C. | 重力对物体做功180J | D. | 物体的动能增加了62J |
10.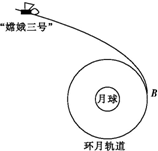 2013年12月14日,“嫦娥三号”探月卫星在月面成功实现软着陆.如图所示,在月球椭圆轨道上的已关闭动力的探月卫星在月球引力作用下向月球靠近,并在B处变轨进入半径为r、周期为T的环月轨道运行,后经过多次调整,最后安全着陆.已知引力常量为G,下列理解正确的是( )
2013年12月14日,“嫦娥三号”探月卫星在月面成功实现软着陆.如图所示,在月球椭圆轨道上的已关闭动力的探月卫星在月球引力作用下向月球靠近,并在B处变轨进入半径为r、周期为T的环月轨道运行,后经过多次调整,最后安全着陆.已知引力常量为G,下列理解正确的是( )
 2013年12月14日,“嫦娥三号”探月卫星在月面成功实现软着陆.如图所示,在月球椭圆轨道上的已关闭动力的探月卫星在月球引力作用下向月球靠近,并在B处变轨进入半径为r、周期为T的环月轨道运行,后经过多次调整,最后安全着陆.已知引力常量为G,下列理解正确的是( )
2013年12月14日,“嫦娥三号”探月卫星在月面成功实现软着陆.如图所示,在月球椭圆轨道上的已关闭动力的探月卫星在月球引力作用下向月球靠近,并在B处变轨进入半径为r、周期为T的环月轨道运行,后经过多次调整,最后安全着陆.已知引力常量为G,下列理解正确的是( )| A. | 图中探月卫星在飞向B处的过程中,加速度增大 | |
| B. | 探月卫星要进入环月轨道应在B处减速 | |
| C. | 探月卫星在接近月球表面前只受万有引力作用,应加速着陆 | |
| D. | 由题中条件可以计算出月球的质量 |
17.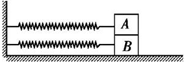 如图所示,质量相等的物块A、B叠放在光滑水平面上.两原长相同的轻质弹簧的一端均固定在竖直墙壁上,另一端分别与A、B相连接.设与A相连的弹簧的劲度系数为kA,与B相连的弹簧的劲度系数为kB,开始时A、B均处于静止状态.现对物块B施加一水平向右的拉力,使A、B一起向右移动到某一位置后再次处于静止状态,在移动过程中A、B无相对滑动,弹簧处于弹性限度内,则撤去这个拉力后( )
如图所示,质量相等的物块A、B叠放在光滑水平面上.两原长相同的轻质弹簧的一端均固定在竖直墙壁上,另一端分别与A、B相连接.设与A相连的弹簧的劲度系数为kA,与B相连的弹簧的劲度系数为kB,开始时A、B均处于静止状态.现对物块B施加一水平向右的拉力,使A、B一起向右移动到某一位置后再次处于静止状态,在移动过程中A、B无相对滑动,弹簧处于弹性限度内,则撤去这个拉力后( )
 如图所示,质量相等的物块A、B叠放在光滑水平面上.两原长相同的轻质弹簧的一端均固定在竖直墙壁上,另一端分别与A、B相连接.设与A相连的弹簧的劲度系数为kA,与B相连的弹簧的劲度系数为kB,开始时A、B均处于静止状态.现对物块B施加一水平向右的拉力,使A、B一起向右移动到某一位置后再次处于静止状态,在移动过程中A、B无相对滑动,弹簧处于弹性限度内,则撤去这个拉力后( )
如图所示,质量相等的物块A、B叠放在光滑水平面上.两原长相同的轻质弹簧的一端均固定在竖直墙壁上,另一端分别与A、B相连接.设与A相连的弹簧的劲度系数为kA,与B相连的弹簧的劲度系数为kB,开始时A、B均处于静止状态.现对物块B施加一水平向右的拉力,使A、B一起向右移动到某一位置后再次处于静止状态,在移动过程中A、B无相对滑动,弹簧处于弹性限度内,则撤去这个拉力后( )| A. | 若kA=kB,则A、B间不存在摩擦力作用 | |
| B. | 若kA>kB,则A受到向左的摩擦力作用 | |
| C. | 若kA<kB,则A受到的摩擦力方向始终与弹簧对它的弹力方向相同 | |
| D. | 若kA<kB,则A受到的摩擦力与弹簧对它的弹力方向有时相同,有时相反 |
7.下列有关晶体和非晶体的说法中正确的是( )
| A. | 非晶体具有各向同性,单晶体和多晶体都具有各向异性 | |
| B. | 多晶体没有确定的几何形状,但有固定的熔点 | |
| C. | 玻璃没有确定的熔点,也没有规则的几何形状,所以玻璃是非晶体 | |
| D. | 同一种物质不可能以晶体和非晶体两种不同的形态出现 |
11. 如图所示,带支架的平板小车沿水平面向左作直线运动.小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端.B与小车平板间的动摩擦因数为μ.若某时刻观察到细线偏离竖直方向θ角,则此刻小车对物块B产生的作用力的大小和方向为( )
如图所示,带支架的平板小车沿水平面向左作直线运动.小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端.B与小车平板间的动摩擦因数为μ.若某时刻观察到细线偏离竖直方向θ角,则此刻小车对物块B产生的作用力的大小和方向为( )
 如图所示,带支架的平板小车沿水平面向左作直线运动.小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端.B与小车平板间的动摩擦因数为μ.若某时刻观察到细线偏离竖直方向θ角,则此刻小车对物块B产生的作用力的大小和方向为( )
如图所示,带支架的平板小车沿水平面向左作直线运动.小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端.B与小车平板间的动摩擦因数为μ.若某时刻观察到细线偏离竖直方向θ角,则此刻小车对物块B产生的作用力的大小和方向为( )| A. | mg$\sqrt{1+tan{θ}^{2}}$,斜向右上方 | B. | mg,斜向左上方 | ||
| C. | mgtanθ,水平向右 | D. | mg,竖直向上 |