题目内容
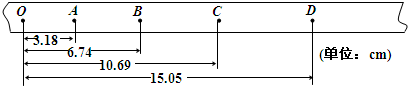
某同学利用打点计时器所记录的纸带来研究做匀变速直线运动小车的运动情况，实验中获得一条纸带，如图所示，其中两相邻计数点间有四个点未画出．已知所用电源的频率为50Hz，则打O点时小车运动的速度v0=
0.298
0.298
m/s，小车运动的加速度a=0.393
0.393
m/s2．（结果要求保留三位有效数字）分析：根据某段时间内平均速度等于中间时刻的瞬时速度求出A点的瞬时速度，通过逐差法，运用相邻相等时间内的位移之差是一恒量求出加速度，通过速度时间公式求出O点的速度．
解答：解：由于两相邻计数点间有四个点未画出，所以两相邻计数点时间间隔为0.1s
利用匀变速直线运动的推论得：vA=
=
=0.337m/s．
由于相邻的时间间隔位移之差不相等，
根据运动学公式推论△x=aT2采用逐差法得出：
a=
=
=0.393m/s2．
则O点的速度v0=vA-aT=0.337-0.393×0.1≈0.298m/s．
故答案为：0.298 0.393
利用匀变速直线运动的推论得：vA=
| xOB |
| 2T |
| 6.74×10-2 |
| 0.2 |
由于相邻的时间间隔位移之差不相等，
根据运动学公式推论△x=aT2采用逐差法得出：
a=
| xBC+xCD-xOA-xAB |
| 4T2 |
| [(15.05-6.74)-6.74]×10-2 |
| 4×0.01 |
则O点的速度v0=vA-aT=0.337-0.393×0.1≈0.298m/s．
故答案为：0.298 0.393
点评：能够知道相邻的计数点之间的时间间隔．要注意单位的换算和有效数字的保留．了解逐差法求解加速度有利于减小误差．
练习册系列答案
相关题目
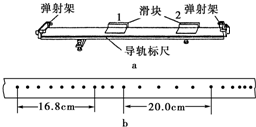（2009?肇庆一模）某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验．气垫导轨装置如图a所示，所用的气垫导轨装置由导轨、滑块、弹射架等组成．在空腔导轨的两个工作面上均匀分布着一定数量的小孔，向导轨空腔内不断通入压缩空气，空气会从小孔中喷出，使滑块稳定地漂浮在导轨上，这样就大大减小了因滑块和导轨之间的摩擦而引起的误差．
