题目内容
【题目】如图所示,水池正上方有一小球,球距水面h1=3.2m,池水深h2=1.6m,小球从静止释放后落入水中做减速运动,到池底的速度恰好为零,(取g=10m/s2)求: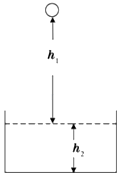
(1)小球运动的最大速度;
(2)小球在水中运动的加速度;
(3)从开始到落到池底所用的时间.
【答案】
(1)
解:小球下落到水面时速度最大且为vm,由速度与位移公式: ![]()
代入数据解得:vm=8m/s
(2)
解:设小球在水池中减速运动的加速度大小为a,由速度位移关系有: ![]()
代入数据解得:a=20m/s2 方向竖直向上
(3)
解:小球下落到水面的时间为t1,由自由落体公式: ![]()
代入数据解得:t1=0.8s
减速运动的时间为t2,0=vm﹣at2
由以上两式代入数据可解得:t2=0.4s
所以运动总时间:t=t1+t2=1.2s
【解析】(1)小球在入水之前做自由落体运动,入水后做匀减速运动,故速度最大是自由落体运动的末速度;(2)根据速度位移公式求小球在水中运动的加速度;(3)由自由落体求得水上运动时间,根据匀变速直线运动的速度位移关系由初速度、末速度和位移求得水中的加速度,再根据速度时间关系求得时间.
【考点精析】解答此题的关键在于理解自由落体运动的相关知识,掌握(1)条件:初速度为零,只受重力作用;(2)性质:是一种初速为零的匀加速直线运动,a=g.

【题目】用打点计时器测定匀变速直线运动的加速度的实验时记录下的一条纸带,纸带上选取1、2、3、4、5各点为记数点,将直尺靠在纸带边,零刻线与纸带上某一点0对齐,由0到l、2、3…点的距离分别用d1、d2、d3…表示,测量出d1、d2、d3…的值,已知打点计时器所用交流电的频率为50Hz,由测量数据计算出小车的加速度a和纸带上打下点3时小车的速度v3 , 并说明加速度的方向.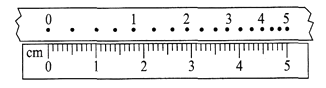
(1)补全下表
距离 | d1 | d2 | d3 | d4 | d5 |
测量值(cm) |
(2)加速度a=m/s2(保留两位有效数),加速度的方向与运动方向(填“相同”或“相反”),小车在点3时的速度大小v3=m/s(保留两位有效数).