题目内容
 (2011?湛江模拟)如图所示,足够长的水平粗糙轨道与固定在水平面上的光滑弧形轨道在P点相切,质量为m的滑块B静止于P点;质量为2m的滑块A由静止开始沿着光滑弧形轨道下滑,下滑的起始位置距水平轨道的高度为h,滑块A在P点与静止的滑块B碰撞后,两滑块粘合在一起共同向左运动.两滑块均可视为质点,且与水平轨道的动摩擦因素均为μ,P点切线水平.求:
(2011?湛江模拟)如图所示,足够长的水平粗糙轨道与固定在水平面上的光滑弧形轨道在P点相切,质量为m的滑块B静止于P点;质量为2m的滑块A由静止开始沿着光滑弧形轨道下滑,下滑的起始位置距水平轨道的高度为h,滑块A在P点与静止的滑块B碰撞后,两滑块粘合在一起共同向左运动.两滑块均可视为质点,且与水平轨道的动摩擦因素均为μ,P点切线水平.求:(1)滑块A到达P点与B碰前瞬间的速度大小;
(2)两滑块最终停止时距P点的距离.
分析:(1)、弧形轨道光滑,所以滑块A在沿弧形轨道下滑至于B碰撞前机械能守恒,应用机械能守恒定律即可求出滑块A到达P点与B碰前瞬间的速度.
(2)、在P点AB两物体发生碰撞,在碰撞过程中,动量守恒,可由动量守恒定律求出碰撞后两物体的共同速度;碰后AB在粗糙的水平轨道上滑行,做匀减速直线运动,碰后的动能转化为内能,由能量的转化与守恒可求出滑行的距离.
(2)、在P点AB两物体发生碰撞,在碰撞过程中,动量守恒,可由动量守恒定律求出碰撞后两物体的共同速度;碰后AB在粗糙的水平轨道上滑行,做匀减速直线运动,碰后的动能转化为内能,由能量的转化与守恒可求出滑行的距离.
解答:解:
(1)设滑块A到达P点与B碰前瞬间的速度为v0,由机械能守恒定律有:
2mgh=
?2m
解得ν0=
(2)设滑块A与B碰撞后的共同速度为v,由动量守恒定律有:
2mv0=3mv
两滑块粘合在-起共同向左运动,设最终停止时距P点的距离为s,由动能定理有
μ?3mgs=
?3mν2
联立上述式子并代入数据解得:
s=
答:(1)滑块A到达P点与B碰前瞬间的速度为
.
(2)两滑块最终停止时距P点的距离为
.
(1)设滑块A到达P点与B碰前瞬间的速度为v0,由机械能守恒定律有:
2mgh=
| 1 |
| 2 |
| ν | 2 0 |
解得ν0=
| 2gh |
(2)设滑块A与B碰撞后的共同速度为v,由动量守恒定律有:
2mv0=3mv
两滑块粘合在-起共同向左运动,设最终停止时距P点的距离为s,由动能定理有
μ?3mgs=
| 1 |
| 2 |
联立上述式子并代入数据解得:
s=
| 4h |
| 9μ |
答:(1)滑块A到达P点与B碰前瞬间的速度为
| 2gh |
(2)两滑块最终停止时距P点的距离为
| 4h |
| 9μ |
点评:应用机械能守恒定律解题,可从两个方面分析守恒的条件:一是只有重力(或系统内弹力)做功,其他外力和内力不做功(或其他力做功的代数和为零).二是物体间只有动能和势能的相互转化,系统与外界没有发生机械能的传递,机械能也没有转化为其他形式的能.
物体在粗糙的水平面上滑动,由于有摩擦力存在,物体会做匀减速直线运动,此过程中摩擦力做功,使机械能转化为系统的内能.应用摩擦力做功求解机械能能的转化时,要注意摩擦力与相对位移的乘积才是转化为内能的部分.
此题的第二问还可由牛顿运动定律和运动学公式求解.
物体在粗糙的水平面上滑动,由于有摩擦力存在,物体会做匀减速直线运动,此过程中摩擦力做功,使机械能转化为系统的内能.应用摩擦力做功求解机械能能的转化时,要注意摩擦力与相对位移的乘积才是转化为内能的部分.
此题的第二问还可由牛顿运动定律和运动学公式求解.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
 (2011?湛江模拟)如图所示,在磁感应强度B=1.2T的匀强磁场中,让导体PQ在U型导轨上以速度υ0=10m/s向右匀速滑动,两导轨间距离L=0.5m,则产生的感应电动势的大小和PQ中的电流方向分别为( )
(2011?湛江模拟)如图所示,在磁感应强度B=1.2T的匀强磁场中,让导体PQ在U型导轨上以速度υ0=10m/s向右匀速滑动,两导轨间距离L=0.5m,则产生的感应电动势的大小和PQ中的电流方向分别为( ) (2011?湛江模拟)甲、乙两车在某时刻由同一地点沿同一方向开始做直线运动,若以该时刻作为计时起点,得到两车的速度一时间图象如图所示.则下列说法正确的是( )
(2011?湛江模拟)甲、乙两车在某时刻由同一地点沿同一方向开始做直线运动,若以该时刻作为计时起点,得到两车的速度一时间图象如图所示.则下列说法正确的是( )
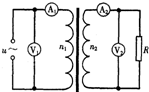 (2011?湛江模拟)如图所示,理想变压器的原线圈匝数为n1=l000匝,副线圈匝数为n2=200匝,交变电源的电动势
(2011?湛江模拟)如图所示,理想变压器的原线圈匝数为n1=l000匝,副线圈匝数为n2=200匝,交变电源的电动势