题目内容
 (2008?江苏模拟)如图所示,圆形区域内有垂直纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同的速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图.若带电粒子只受磁场力的作用,则下列说法正确的是( )
(2008?江苏模拟)如图所示,圆形区域内有垂直纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同的速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图.若带电粒子只受磁场力的作用,则下列说法正确的是( )分析:三个质量和电荷量都相同的带电粒子,以不同的速率垂直进入匀强磁场中,则运动半径的不同,导致运动轨迹也不同.运动轨迹对应的半径越大,粒子的速率也越大.而运动周期它们均一样,运动时间由圆弧对应的圆心角决定.
解答:解:A、B粒子在磁场中做匀速圆周运动时,由洛伦兹力提供向心力,根据qvB=m
,可得:r=
,粒子的动能Ek=
mv2,则可知三个带电粒子的质量、电荷量相同,在同一个磁场中,当速度越大时、轨道半径越大,则由图知,a粒子速率最小,c粒子速率最大.c粒子动能最大.故A错误,B正确.
C、由于粒子运动的周期T=
及t=
T可知,三粒子运动的周期相同,a在磁场中运动的偏转角最大,运动的时间最长,故C正确、D错误.
故选B
| v2 |
| r |
| mv |
| qB |
| 1 |
| 2 |
C、由于粒子运动的周期T=
| 2πm |
| qB |
| θ |
| 2π |
故选B
点评:带电粒子在磁场、质量及电量相同情况下,运动的半径与速率成正比,从而根据运动圆弧来确定速率的大小;运动的周期均相同的情况下,可根据圆弧的对应圆心角来确定运动的时间的长短.

练习册系列答案
相关题目
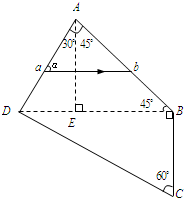 (2008?江苏模拟)如图所示,玻璃棱镜ABCD可以看成是由ADE、ABE、BCD三个直角三棱镜组成.一束频率为5.3×1014Hz的单色细光束从AD面入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角α=60°.己知光在真空中的速度c=3×108m/s,玻璃的折射率n=1.5,求:
(2008?江苏模拟)如图所示,玻璃棱镜ABCD可以看成是由ADE、ABE、BCD三个直角三棱镜组成.一束频率为5.3×1014Hz的单色细光束从AD面入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角α=60°.己知光在真空中的速度c=3×108m/s,玻璃的折射率n=1.5,求: (2008?江苏模拟)如图所示,可视为质点的物块A放在物体B上,A、B之间有摩擦,水平地面光滑.现将物块A从物体B的顶端由静止释放,在滑到物体B的底端前,下列说法正确的是( )
(2008?江苏模拟)如图所示,可视为质点的物块A放在物体B上,A、B之间有摩擦,水平地面光滑.现将物块A从物体B的顶端由静止释放,在滑到物体B的底端前,下列说法正确的是( ) (2008?江苏模拟)如图所示,用一根长为L的细绳一端固定在O点,另一端悬挂质量为m的小球A,为使细绳与竖直方向夹30°角且绷紧,小球A处于静止,则需对小球施加的最小力等于( )
(2008?江苏模拟)如图所示,用一根长为L的细绳一端固定在O点,另一端悬挂质量为m的小球A,为使细绳与竖直方向夹30°角且绷紧,小球A处于静止,则需对小球施加的最小力等于( )