题目内容
把一个质量为 m=0.2kg的小球放在高度为 h=5.0m的直杆的顶端，如图所示，一颗质量为 m'=0.01kg的子弹以速度 v0=500m/s沿水平方向击穿小球，小球落地点与杆的水平距离S=20m．求：（1）子弹落地点距杆的水平距离S'；
（2）子弹落地时的速度．
分析：（1）小球被击穿后做平抛运动，根据高度与水平距离求出子弹击穿小球后的速度．子弹击穿小球的过程，遵守动量守恒，根据动量守恒定律求出击穿后子弹的速度，再由平抛运动的规律求出子弹落地点距杆的水平距离S′．
（2）根据机械能守恒研究子弹平抛运动的过程，即可求解子弹落地时的速度．
（2）根据机械能守恒研究子弹平抛运动的过程，即可求解子弹落地时的速度．
解答：解：（1）小球被击穿后做平抛运动，击穿后的速度为v1，空中飞行时间为t
则：S=v1t ①
h=
gt2 ②
由①②式得 v1=20m/s
击穿过程中，子弹与小球水平方向动量守恒，设击穿后子弹的速度为v2
由动量守恒定律得：m′v0=mv1+m′v2得，
v2=100m/s
由平抛运动的特点知，两球平抛运动的时间相等，则由S=v0t，得：
=
故得S′=100m
（2）对子弹平抛运动的过程，根据机械能守恒得：
mgh+
m
=
m
解得，子弹落地时的速度v2′=
=
m/s
答：
（1）子弹落地点距杆的水平距离S′是100m；
（2）子弹落地时的速度是
m/s．
则：S=v1t ①
h=
| 1 |
| 2 |
由①②式得 v1=20m/s
击穿过程中，子弹与小球水平方向动量守恒，设击穿后子弹的速度为v2
由动量守恒定律得：m′v0=mv1+m′v2得，
v2=100m/s
由平抛运动的特点知，两球平抛运动的时间相等，则由S=v0t，得：
| S′ |
| S |
| v2 |
| v1 |
故得S′=100m
（2）对子弹平抛运动的过程，根据机械能守恒得：
mgh+
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | ′2 2 |
解得，子弹落地时的速度v2′=
2gh+
|
| 10100 |
答：
（1）子弹落地点距杆的水平距离S′是100m；
（2）子弹落地时的速度是
| 10100 |
点评：子弹射击物体过程，基本规律是动量守恒和能量守恒．本题是动量守恒与平抛运动的综合，常规题．
练习册系列答案
相关题目
如图所示，两平行金属导轨间的距离L=0.40m，金属导轨所在的平面与水平面夹角θ=37°，在导轨所在平面内，分布着磁感应强度B=0.50T、方向垂直于导轨所在平面的匀强磁场．金属导轨的一端接有电动势E=4.5V、内阻r=0.50Ω的直流电源，另一端接有电阻R=5.0Ω．现把一个质量为m=0.040kg的导体棒ab放在金属导轨上，导体棒静止．导体棒与金属导轨垂直、且接触良好，与金属导轨接触的两点间的导体棒的电阻R0=5.0Ω，金属导轨电阻不计，g取10m/s2．已知sin37°=0.60，cos37°=0.80，求：
如图所示，两平行金属导轨间的距离L=0.40m，金属导轨所在的平面与水平面夹角θ=37°，在导轨所在平面内，分布着磁感应强度B=0.50T、方向垂直于导轨所在平面的匀强磁场．金属导轨的一端接有电动势E=4.5V、内阻r=0.50Ω的直流电源，另一端接有电阻R=5.0Ω．现把一个质量为m=0.040kg的导体棒ab放在金属导轨上，导体棒静止．导体棒与金属导轨垂直、且接触良好，与金属导轨接触的两点间的导体棒的电阻R0=5.0Ω，金属导轨电阻不计，g取10m/s2．已知sin37°=0.60，cos37°=0.80，求：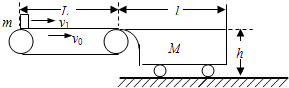
（2010?成都三模）光滑水平面上静止有质量为M=2㎏，长度均为l=1m的平顶小车，小车右端有一挡板，小车紧靠在长为L=1.5m的水平传送带的右端，其上表面与传送带等高，与光滑水平面的高度h=0.8m，如图所示．当传送带以恒定的速度v0=5m/s运动时，把一个质量为m=0.5kg的小滑块（可当作质点）以某初速度滑上传送带的左端，以后小滑块恰好能经传送带一直加速而滑到小车上．已知小滑块与传送带的动摩擦因数μ1=0.3，与小车表面的动摩擦因数μ2=0.1，g=10m/s2．试求：
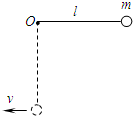用一根长为l=0.8m的轻质不可伸长的细绳把一个质量为m=0.2kg的小球悬挂在点O，将小球拉至与悬点等高处由静止释放，如图所示（g取10m/s2）．求：
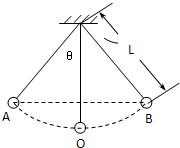如图，把一个质量为m=0.05kg的小球用细线悬挂起来，就成为一个摆，摆长为L，最大偏角为60°，重力加速度为g，求小球运动到最低点O时对细线的拉力．