题目内容
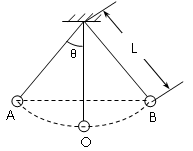
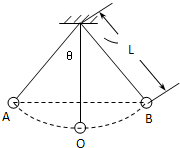如图，把一个质量为m=0.05kg的小球用细线悬挂起来，就成为一个摆，摆长为L，最大偏角为60°，重力加速度为g，求小球运动到最低点O时对细线的拉力．分析：小球在摆动的过程中，只有重力做功，机械能守恒，根据机械能守恒定律求出小球运动到最低位置时的速度大小．在最低点，小球靠重力和拉力的合力提供向心力，根据牛顿第二定律求出细线的拉力大小．
解答：解：由偏角θ为60°释放小球到最低点时，竖直的高度差是：
h=l（1-cos60°）=L×（1-0.5）m=0.5L（m）
此过程，根据机械能守恒定律知：mgh=
mv2
所以有：v=
=
m/s=
m/s
在最低点O，合外力提供向心力，有：F合=F向
则得：F拉-mg=
解得：F拉=mg+
=2mg=2×0.05×10N=1N
答：小球运动到最低点O时对细线的拉力为1N．
h=l（1-cos60°）=L×（1-0.5）m=0.5L（m）
此过程，根据机械能守恒定律知：mgh=
| 1 |
| 2 |
所以有：v=
| 2gh |
| 2g×0.5L |
| gL |
在最低点O，合外力提供向心力，有：F合=F向
则得：F拉-mg=
| mv2 |
| L |
解得：F拉=mg+
| mgL |
| L |
答：小球运动到最低点O时对细线的拉力为1N．
点评：本题综合考查了机械能守恒定律和牛顿第二定律，难度不大，需加强这方面的训练，基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
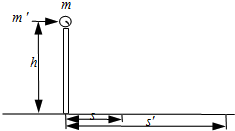（2004?青岛一模）把一个质量为 m=0.2 0kg的小球放在高度为 h=5.0m的直杆的顶端，如图所示，一颗质量为m′=0.01kg的子弹以速度 v0=500m/s沿水平方向击穿小球，小球落地点与杆的水平距离S=20m．
如图所示，两平行金属导轨间的距离L=0.40m，金属导轨所在的平面与水平面夹角θ=37°，在导轨所在平面内，分布着磁感应强度B=0.50T、方向垂直于导轨所在平面的匀强磁场．金属导轨的一端接有电动势E=4.5V、内阻r=0.50Ω的直流电源，另一端接有电阻R=5.0Ω．现把一个质量为m=0.040kg的导体棒ab放在金属导轨上，导体棒静止．导体棒与金属导轨垂直、且接触良好，与金属导轨接触的两点间的导体棒的电阻R0=5.0Ω，金属导轨电阻不计，g取10m/s2．已知sin37°=0.60，cos37°=0.80，求：
（2010?海淀区模拟）如图所示，质量为m的小球用长为L的悬线固定于O点，在O点正下方O′处钉一个钉子，把悬线拉直与竖直方向成一定角度，由静止释放小球，当悬线碰到钉子时，则（ ）
