题目内容
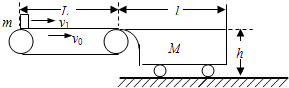 (2010?成都三模)光滑水平面上静止有质量为M=2㎏,长度均为l=1m的平顶小车,小车右端有一挡板,小车紧靠在长为L=1.5m的水平传送带的右端,其上表面与传送带等高,与光滑水平面的高度h=0.8m,如图所示.当传送带以恒定的速度v0=5m/s运动时,把一个质量为m=0.5kg的小滑块(可当作质点)以某初速度滑上传送带的左端,以后小滑块恰好能经传送带一直加速而滑到小车上.已知小滑块与传送带的动摩擦因数μ1=0.3,与小车表面的动摩擦因数μ2=0.1,g=10m/s2.试求:
(2010?成都三模)光滑水平面上静止有质量为M=2㎏,长度均为l=1m的平顶小车,小车右端有一挡板,小车紧靠在长为L=1.5m的水平传送带的右端,其上表面与传送带等高,与光滑水平面的高度h=0.8m,如图所示.当传送带以恒定的速度v0=5m/s运动时,把一个质量为m=0.5kg的小滑块(可当作质点)以某初速度滑上传送带的左端,以后小滑块恰好能经传送带一直加速而滑到小车上.已知小滑块与传送带的动摩擦因数μ1=0.3,与小车表面的动摩擦因数μ2=0.1,g=10m/s2.试求:(1)小滑块滑上传送带的瞬时的速度大小v1;
(2)若小滑块与小车右端的挡板相碰时,时间极短,且无机械能损失,试判断滑块最后能否相对小车静止,若能,求滑块相对小车静止时离小车右端的距离;若不能,求滑块落地时离小车右端的水平距离d.(取
| 12.8 |
分析:1、由动能定理列出等式求解.
2、小滑块滑上小车后,由动量守恒定律和功能关系列出等式判断小滑块是否从小车的左端离开小车,
再运用动量守恒定律和功能关系求解.
2、小滑块滑上小车后,由动量守恒定律和功能关系列出等式判断小滑块是否从小车的左端离开小车,
再运用动量守恒定律和功能关系求解.
解答:解:(1)由动能定理得:
-μ1mgL=
m
-
m
解得:v1=4m/s
(2)小滑块滑上小车后,假设能与小车相对静止,且设此时的速度为v2.则:
由动量守恒定律:mv0=(m+M)v2
由功能关系:
m
=
(m+M)
+μ2mgs
求解上述两式得:s=10m>2l=2m
故假设不成立,即小滑块要从小车的左端离开小车.
设小滑块离开小车的速度为v3,小车的速度为v4.同理
由动量守恒定律:mv0=mv3+Mv4
由功能关系:
m
=
m
+
M
+μ2mg2l
解得:v3=4.6m/s v4=0.1m/s (舍去)
v3=-2.6m/s v4=1.9m/s
离开小车后小滑块向左做平抛运动,小车向右匀速,
二者的时间由:h=
gt2
得:t=0.4s
故小滑块落地时与小车右端相距d=l+(-v3+v4)t=2.28m
答:(1)小滑块滑上传送带的瞬时的速度大小是4m/s;
(2)小滑块要从小车的左端离开小车,滑块落地时离小车右端的水平距离是2.28m.
-μ1mgL=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
解得:v1=4m/s
(2)小滑块滑上小车后,假设能与小车相对静止,且设此时的速度为v2.则:
由动量守恒定律:mv0=(m+M)v2
由功能关系:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 2 |
求解上述两式得:s=10m>2l=2m
故假设不成立,即小滑块要从小车的左端离开小车.
设小滑块离开小车的速度为v3,小车的速度为v4.同理
由动量守恒定律:mv0=mv3+Mv4
由功能关系:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 3 |
| 1 |
| 2 |
| v | 2 4 |
解得:v3=4.6m/s v4=0.1m/s (舍去)
v3=-2.6m/s v4=1.9m/s
离开小车后小滑块向左做平抛运动,小车向右匀速,
二者的时间由:h=
| 1 |
| 2 |
得:t=0.4s
故小滑块落地时与小车右端相距d=l+(-v3+v4)t=2.28m
答:(1)小滑块滑上传送带的瞬时的速度大小是4m/s;
(2)小滑块要从小车的左端离开小车,滑块落地时离小车右端的水平距离是2.28m.
点评:本题主要考查了动量守恒定律,功能关系,平抛运动规律的应用,关键是清楚物体运动的过程,选择合适的规律进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2010?成都三模)华裔科学家高锟获得2009年诺贝尔物理奖,他被誉为“光纤通讯之父”. 光纤通讯中信号传播的主要载体是光导纤维,它的结构如图所示,其内芯和外套材料不同,光在内芯中传播.下列关于光导纤维的说法中正确的是( )
(2010?成都三模)华裔科学家高锟获得2009年诺贝尔物理奖,他被誉为“光纤通讯之父”. 光纤通讯中信号传播的主要载体是光导纤维,它的结构如图所示,其内芯和外套材料不同,光在内芯中传播.下列关于光导纤维的说法中正确的是( ) (2010?成都三模)美国物理学家劳伦斯于1932年发明的回旋加速器,应用带电粒子在磁场中做 圆周运动的特点,能使粒子在较小的空间范围内经过电场的多次加速获得较大的能量,使人类在获得较高能量带电粒子方面前进了一步.下图为一种改进后的回旋加速器示意图,其中盒缝间的加速电场场强大小恒定,且被限制在A、C板间,如图所示.带电粒子从P0处以速度v0沿电场线方向射入加速电场,经加速后再进入D型盒中的匀强磁场做匀速圆周运动.对于这种改进后的回旋加速器,下列说法正确的是( )
(2010?成都三模)美国物理学家劳伦斯于1932年发明的回旋加速器,应用带电粒子在磁场中做 圆周运动的特点,能使粒子在较小的空间范围内经过电场的多次加速获得较大的能量,使人类在获得较高能量带电粒子方面前进了一步.下图为一种改进后的回旋加速器示意图,其中盒缝间的加速电场场强大小恒定,且被限制在A、C板间,如图所示.带电粒子从P0处以速度v0沿电场线方向射入加速电场,经加速后再进入D型盒中的匀强磁场做匀速圆周运动.对于这种改进后的回旋加速器,下列说法正确的是( ) (2010?成都三模)如图所示,一半圆形铝框处在水平向外的非匀强磁场中,场中各点的磁感强度为
(2010?成都三模)如图所示,一半圆形铝框处在水平向外的非匀强磁场中,场中各点的磁感强度为