题目内容
(2007?上海模拟)如图所示,一根轻绳一端系一个小球,另一端固定在O点,在O点有一个能测量绳的拉力的测力传感器E,让小球绕O点在竖直平面内做圆周运动,如图(a)所示.由传感器测出拉力F随时间t的变化图象如图(b)所示.已知小球在最低点A的速度vA=6m/s.求
(1)小球圆周运动周期;
(2)小球的质量;
(3)轻绳的长度L;
(4)小球在最高点的动能.

(1)小球圆周运动周期;
(2)小球的质量;
(3)轻绳的长度L;
(4)小球在最高点的动能.
分析:小球在竖直平面内做简谐运动,在最低点绳子的拉力和重力的合力提供向心力,此时拉力最大;在最大位移处,绳子的拉力等于重力的一个分力,此时拉力最小.根据在一次全振动中两次经过平衡位置,求出小球的周期.速度的变化的周期等于小球运动的周期.根据牛顿第二定律与小球的机械能守恒定律,可列出方程求出小球的质量与轻绳的长度.再由动能定理可求出小球在最高点的动能.
解答: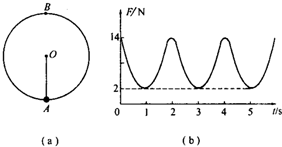 解:(1)由F与t的图象关系可知:小球圆周运动周期为2s
解:(1)由F与t的图象关系可知:小球圆周运动周期为2s
(2)当小球在最高点时,绳子的拉力最小;小球在最低点时,绳子的拉力最大.且小球从最低点到最高点过程中只有重力做功,所以小球的机械能守恒.
则有:最高点G+F小=m
最低点F大-G=m
最低点到最高点,机械能守恒定律:
m
=
m
+mg?2R
由上三式可得:小球的质量m=0.2kg
(3)轻绳的长度L=R=0.6m
(4)小球在最高点的动能Ek=
m
-mg?2R=1.2J
答:(1)小球圆周运动周期2s;
(2)小球的质量0.2kg;
(3)轻绳的长度0.6m;
(4)小球在最高点的动能1.2J.
 解:(1)由F与t的图象关系可知:小球圆周运动周期为2s
解:(1)由F与t的图象关系可知:小球圆周运动周期为2s(2)当小球在最高点时,绳子的拉力最小;小球在最低点时,绳子的拉力最大.且小球从最低点到最高点过程中只有重力做功,所以小球的机械能守恒.
则有:最高点G+F小=m
| ||
| R |
最低点F大-G=m
| ||
| R |
最低点到最高点,机械能守恒定律:
| 1 |
| 2 |
| v | 2 低 |
| 1 |
| 2 |
| v | 2 高 |
由上三式可得:小球的质量m=0.2kg
(3)轻绳的长度L=R=0.6m
(4)小球在最高点的动能Ek=
| 1 |
| 2 |
| v | 2 低 |
答:(1)小球圆周运动周期2s;
(2)小球的质量0.2kg;
(3)轻绳的长度0.6m;
(4)小球在最高点的动能1.2J.
点评:由图象读出信息是本题解题的突破口,再由牛顿第二定律与机械能守恒定律,并结合向心力公式,从而培养学生分析与解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
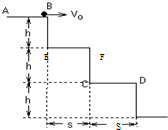 (2007?上海模拟)如图所示,三个台阶每个台阶高h=0.225米,宽s=0.3米.小球在平台AB上以初速度v0水平向右滑出,要使小球正好落在第2个平台CD上,不计空气阻力,求初速v0范围.某同学计算如下:(g取10m/s2)
(2007?上海模拟)如图所示,三个台阶每个台阶高h=0.225米,宽s=0.3米.小球在平台AB上以初速度v0水平向右滑出,要使小球正好落在第2个平台CD上,不计空气阻力,求初速v0范围.某同学计算如下:(g取10m/s2) (2007?上海模拟)在做“研究有固定转动轴物体平衡条件”的实验过程中,检验力矩盘的重心是否位于盘中心的方法是
(2007?上海模拟)在做“研究有固定转动轴物体平衡条件”的实验过程中,检验力矩盘的重心是否位于盘中心的方法是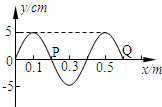 (2007?上海模拟)如图所示,是一列简谐横波在t=0时的波形图,若波的传播速度为2m/s,则下列说法中正确的是( )
(2007?上海模拟)如图所示,是一列简谐横波在t=0时的波形图,若波的传播速度为2m/s,则下列说法中正确的是( )