题目内容
(2007?上海模拟)在“用单摆测定重力加速度”的实验中
(1)用刻度尺量出悬点到小球的距离96.60cm,已量得小球直径是5.26cm,某同学为减少实验误差,对同一摆长的单摆进行3次周期测量,每次是在摆球通过最低点时,按下秒表开始计时,同时将此次通过最低点作为第一次,接着记录通过最低点的次数,一直数到计时终止,结果如下表:
这个单摆振动周期的测定值是
(2)若测得的g值比实际值大,则可能的原因是
(A)摆球的质量过大 (B)秒表走时比标准钟慢
(C)将振动次数n错记为(n+1)(D)测摆长时未计入摆球的半径.
(1)用刻度尺量出悬点到小球的距离96.60cm,已量得小球直径是5.26cm,某同学为减少实验误差,对同一摆长的单摆进行3次周期测量,每次是在摆球通过最低点时,按下秒表开始计时,同时将此次通过最低点作为第一次,接着记录通过最低点的次数,一直数到计时终止,结果如下表:
| 1 | 2 | 3 | |
| 数的次数 | 61 | 71 | 81 |
| 时间(s) | 60.40 | 70.60 | 79.80 |
2.01
2.01
s,当地重力加速度的值是9.70
9.70
m/s2(小数点后保留两位).(2)若测得的g值比实际值大,则可能的原因是
BC
BC
(A)摆球的质量过大 (B)秒表走时比标准钟慢
(C)将振动次数n错记为(n+1)(D)测摆长时未计入摆球的半径.
分析:(1)每次都在摆球通过最低点时按下秒表开始计时,同时将此次通过最低点作为第一次,以后每两次通过平衡位置,单摆完成一次全振动.确定全振动的次数,求出周期.由单摆的周期公式求解当地重力加速度.
(2)根据单摆周期公式求出重力加速度的表达式,然后分析实验误差.
(2)根据单摆周期公式求出重力加速度的表达式,然后分析实验误差.
解答:解:(1)根据题意与表中实验数据可得:第1次,次数n1=61,全振动的次数为N1=
=30次,
周期T1=
s=2.01s,同理可求出,T2=2.00s,T3=2.02s,周期的平均值为T=
(T1+T2+T3)=2.01s;
摆长L=96.60cm+
×5.26cm=0.9923m,
由T=2π
得:g=
,
代入数据,解得:g≈9.70m/s2;
(2)周期T=
,单摆摆长L=l+
,由T=2π
得:g=
=
,
A、由表达式可知,g与摆球质量无关,故A错误;
B、秒表走时比标准钟慢,t偏小,故g偏大,故B正确;
C、将振动次数n错记为(n+1),重力加速度偏大,故C正确;
D、测摆长时未计入摆球的半径,g偏小,故D错误;
故答案为:(1)2.01;9.70;(2)BC.
| 61-1 |
| 2 |
周期T1=
| 60.40 |
| 30 |
| 1 |
| 3 |
摆长L=96.60cm+
| 1 |
| 2 |
由T=2π
|
| 4π2L |
| T2 |
代入数据,解得:g≈9.70m/s2;
(2)周期T=
| t |
| n |
| d |
| 2 |
|
| 4π2L |
| T2 |
4π2n2(l+
| ||
| t2 |
A、由表达式可知,g与摆球质量无关,故A错误;
B、秒表走时比标准钟慢,t偏小,故g偏大,故B正确;
C、将振动次数n错记为(n+1),重力加速度偏大,故C正确;
D、测摆长时未计入摆球的半径,g偏小,故D错误;
故答案为:(1)2.01;9.70;(2)BC.
点评:本题关键要采用多次测量取平均值,来减小测量的偶然误差,不能把一次测量结果作为周期,误差将较大.
求出重力加速度的表达式,根据表达式分析实验误差.
求出重力加速度的表达式,根据表达式分析实验误差.

练习册系列答案
相关题目
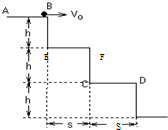 (2007?上海模拟)如图所示,三个台阶每个台阶高h=0.225米,宽s=0.3米.小球在平台AB上以初速度v0水平向右滑出,要使小球正好落在第2个平台CD上,不计空气阻力,求初速v0范围.某同学计算如下:(g取10m/s2)
(2007?上海模拟)如图所示,三个台阶每个台阶高h=0.225米,宽s=0.3米.小球在平台AB上以初速度v0水平向右滑出,要使小球正好落在第2个平台CD上,不计空气阻力,求初速v0范围.某同学计算如下:(g取10m/s2) (2007?上海模拟)在做“研究有固定转动轴物体平衡条件”的实验过程中,检验力矩盘的重心是否位于盘中心的方法是
(2007?上海模拟)在做“研究有固定转动轴物体平衡条件”的实验过程中,检验力矩盘的重心是否位于盘中心的方法是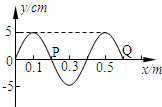 (2007?上海模拟)如图所示,是一列简谐横波在t=0时的波形图,若波的传播速度为2m/s,则下列说法中正确的是( )
(2007?上海模拟)如图所示,是一列简谐横波在t=0时的波形图,若波的传播速度为2m/s,则下列说法中正确的是( )