题目内容
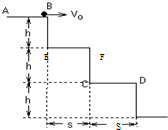 (2007?上海模拟)如图所示,三个台阶每个台阶高h=0.225米,宽s=0.3米.小球在平台AB上以初速度v0水平向右滑出,要使小球正好落在第2个平台CD上,不计空气阻力,求初速v0范围.某同学计算如下:(g取10m/s2)
(2007?上海模拟)如图所示,三个台阶每个台阶高h=0.225米,宽s=0.3米.小球在平台AB上以初速度v0水平向右滑出,要使小球正好落在第2个平台CD上,不计空气阻力,求初速v0范围.某同学计算如下:(g取10m/s2)根据平抛规律
2h=
| 1 |
| 2 |
|
|
到达D点小球的初速 vOD=2s/t=2×0.3/0.3=2m/s
到达C点小球的初速 vOC=s/t=0.3/0.3=1m/s
所以落到台阶CD小球的初速范围是 1m/s<v0<2m/s
以上求解过程是否有问题,若有,指出问题所在,并给出正确的解答.
分析:平抛运动的水平分运动是匀速直线运动,竖直分运动是自由落体运动,根据平抛运动的分位移公式列式求解即可.
解答:解:以上解题有问题,小球无法到达C点.
若要小球恰好落在CD上的最小速度应是小球恰好从F点擦过,落在CD上
所以最小速度 VOF=
=
=
=1.4m/s
所以1.4m/s<V0<2m/s
若要小球恰好落在CD上的最小速度应是小球恰好从F点擦过,落在CD上
所以最小速度 VOF=
| S |
| t/ |
| S | ||||
|
| 0.3 | ||||
|
所以1.4m/s<V0<2m/s
点评:本题关键画出恰好落在第二季台阶上的临界轨迹,然后根据平抛运动的分位移公式列式求解.

练习册系列答案
相关题目
 (2007?上海模拟)在做“研究有固定转动轴物体平衡条件”的实验过程中,检验力矩盘的重心是否位于盘中心的方法是
(2007?上海模拟)在做“研究有固定转动轴物体平衡条件”的实验过程中,检验力矩盘的重心是否位于盘中心的方法是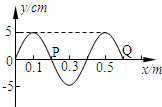 (2007?上海模拟)如图所示,是一列简谐横波在t=0时的波形图,若波的传播速度为2m/s,则下列说法中正确的是( )
(2007?上海模拟)如图所示,是一列简谐横波在t=0时的波形图,若波的传播速度为2m/s,则下列说法中正确的是( )