题目内容
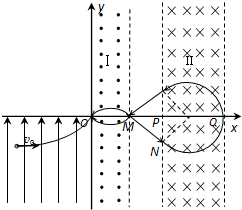
如图所示,在直角坐标系xoy的第一、四象限区域内存在两个有界的匀强磁场:垂直纸面向外的匀强磁场I、垂直纸面向里的匀强磁场II,O、M、P、Q为磁场边界和x轴的交点OM=MP=L.在第三象限存在沿y轴正向的匀强电场.一质量为m、带电荷量为+q的粒子从电场中坐标为(-2L,-L)的点以速度υ0沿+x方向射出,恰好经过原点O处射入区域I又从M点射出区域I(粒子的重力忽略不计).
(1)求第三象限匀强电场场强E的大小;
(2)求区域I内匀强磁场磁感应强度B的大小;
(3)如带电粒子能再次回到原点O,问区域II内磁场的宽度至少为多少?粒子两次经过原点O的时间间隔为多少?

(1)求第三象限匀强电场场强E的大小;
(2)求区域I内匀强磁场磁感应强度B的大小;
(3)如带电粒子能再次回到原点O,问区域II内磁场的宽度至少为多少?粒子两次经过原点O的时间间隔为多少?

(1)带电粒子在匀强电场中做类平抛运动,则有
水平方向:2L=v0t
竖直方向:L=
(
)2
联立解得,E=
(2)设到原点时带电粒子的竖直分速度为vy
则 vy=
t=
=v0
则粒子进入磁场时速度大小为 v=
v0,方向与x轴正向成45°
粒子进入区域Ⅰ做匀速圆周运动,由几何知识可得轨迹半径为 R1=
L
由洛伦兹力充当向心力,则有 Bqv=m
可解得:B=
=
(3)粒子运动轨迹如图.
在区域Ⅱ做匀速圆周的半径为 R2=
L
带电粒子能再次回到原点的条件是区域Ⅱ的宽度d≥R2+L=(
+1)L
粒子从O到M的运动时间t1=
=
粒子从M到N的运动时间t2=
=
粒子在区域Ⅱ中的运动时间t3=
=
粒子两次经过原点O的时间间隔为t总=2(t1+t2)+t3=
答:(1)第三象限匀强电场场强E的大小是
;
(2)区域I内匀强磁场磁感应强度B的大小是
;
(3)如带电粒子能再次回到原点O,区域II内磁场的宽度至少为(
+1)L,粒子两次经过原点O的时间间隔为
.
水平方向:2L=v0t
竖直方向:L=
| 1 |
| 2 |
| qE |
| m |
| 2L |
| v0 |
联立解得,E=
m
| ||
| 2qL |
(2)设到原点时带电粒子的竖直分速度为vy
则 vy=
| qE |
| m |
| qE |
| m |
| 2L |
| v0 |
则粒子进入磁场时速度大小为 v=
| 2 |
粒子进入区域Ⅰ做匀速圆周运动,由几何知识可得轨迹半径为 R1=
| ||
| 2 |
由洛伦兹力充当向心力,则有 Bqv=m
| v2 |
| R1 |
可解得:B=
| mv |
| qR1 |
| 2mv0 |
| qL |
(3)粒子运动轨迹如图.
在区域Ⅱ做匀速圆周的半径为 R2=
| 2 |
带电粒子能再次回到原点的条件是区域Ⅱ的宽度d≥R2+L=(
| 2 |
粒子从O到M的运动时间t1=
| ||||||
|
| πL |
| 4v0 |
粒子从M到N的运动时间t2=
| ||
|
| L |
| v0 |
粒子在区域Ⅱ中的运动时间t3=
| ||||
|
| 3πL |
| 2v0 |
粒子两次经过原点O的时间间隔为t总=2(t1+t2)+t3=
| 2(1+π)L |
| v0 |
答:(1)第三象限匀强电场场强E的大小是
m
| ||
| 2qL |
(2)区域I内匀强磁场磁感应强度B的大小是
| 2mv0 |
| qL |
(3)如带电粒子能再次回到原点O,区域II内磁场的宽度至少为(
| 2 |
| 2(1+π)L |
| v0 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




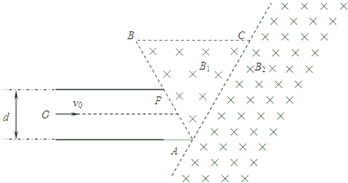 q=-1.0×10-4C;带电粒子恰好从P点垂直AB边以速度v=2×105m/s进入磁场,则
q=-1.0×10-4C;带电粒子恰好从P点垂直AB边以速度v=2×105m/s进入磁场,则