题目内容

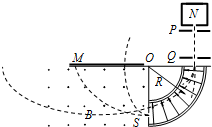
已知某一带负电的粒子以以速度V0垂直进入磁感应强度为B的匀强磁场中，磁场方向垂直于纸面向外，有界磁场的宽度为d，粒子飞出磁场时速度的方向变化了30°，﹙粒子的重力不计﹚求：
（1）该粒子的比荷．
（2）粒子在磁场中飞行的时间．﹙结果均用d、B、V0表示﹚
（1）由粒子轨迹显示的几何关系求得运动半径满足：r=
d
sin30°
=2d-----①
由牛顿第二定律得：qvB=
mv20
r
-----②
由①②得：
q
m
=
v0
2Bd

（2）粒子运动时间为：t=
1
12
×2πr
v0
=
πd
3v0

答：（1）该粒子的比荷为
v0
2Bd

（2）粒子在磁场中飞行的时间为：
πd
3v0
．
练习册系列答案
相关题目
如图示，一个质子以速度v进入匀强磁场中，速度方向与磁场方向垂直．匀强磁场的磁感强度为B，质子的电荷为q，质量为m．质子在洛伦兹力的作用下做匀速圆周运动，用所给的这些物理量，推导出质子在磁场中做圆周运动的半径R的表达式为______．已知磁场的磁感强度B=6.3×10-2T，质子电荷q=1.6×10-19C，质子质量m=1.7×10-27kg，则计算出质子做圆周运动的周期为______s（保留二位有效数字）．
如图所示，在直角坐标系的第三象限有垂直纸面向里的磁感应强度为B0的匀强磁场和竖直向下的电场强度为E0的匀强电场，一系列电荷量为q、质量不同的带负电的粒子（不计重力），沿与x轴平行的水平线通过第三象限电磁场进入y轴右侧垂直纸面向外的磁感应强度为B的匀强磁场中，磁场左边界与y轴重合，磁场右边界与y轴平行且与x轴交于P点，已知OP=L，磁场上下足够长．
（1）求这束带电粒子速度的大小v；
（2）质量满足什么条件的带电粒子能第2次从y轴通过？
（3）如果一种带电粒子与磁场右边界成60°角射出磁场，则带电粒子在磁感应强度为B的匀强磁场中的运动时间是多少？
如图所示，两块平行板电极的长度为L，两板间距离远小于L，可忽略不计．两板的正中央各有一个小孔M、N，两孔连线与板垂直．现将两极板分别接在可调直流电压U的两端，极板处在一有界匀强磁场（板内无磁场），磁感应强度为B，磁场的两条边界CD、DE的夹角θ=60°．极板延长线与边界DE交于Q点，极板最右端P与Q间距离为2.5L．现将比荷均为
q
m
的各种粒子分别从M孔射入电场，不考虑粒子的重力．
（1）若U=U0时，要使带负电的粒子能够从N孔射出，则射入时的初速度v0至少为多少？
（2）将带正电的粒子从M无初速释放，
①若粒子恰好打到下极板右端，求所加直流电压的值U1．
②若U=
2qB2L2
9m
，则该粒子经过多少次电场的加速后可以离开磁场区域？
在磁感应强度为B的匀强磁场中做匀速圆周运动的带电粒子，当磁感应强度突然增大为2B时，这个带电粒子（　　）
A．速率加倍，周期减半
B．速率不变，轨道半径减半
C．速率不变，周期加倍
D．速率减半，轨道半径不变
如图所示，真空中有以O′为圆心，r为半径的圆形匀强磁场区域，磁场方向垂直纸面向外，磁感应强度为B．圆的最下端与x轴相切于直角坐标原点O，圆的右端与平行于y轴的虚线MN相切，在虚线MN右侧x轴上方足够大的范围内有方向竖直向下、场强大小为E的匀强电场，在坐标系第四象限存在方向垂直纸面向里、磁感应强度大小也为B的匀强磁场，现从坐标原点O沿y轴正方向发射速率相同的质子，质子在磁场中做半径为r的匀速圆周运动，然后进入电场到达x轴上的C点．已知质子带电量为+q，质量为m，不计质子的重力、质子对电磁场的影响及质子间的相互作用力．求：
（1）质子刚进入电场时的速度方向和大小；
（2）OC间的距离；
（3）若质子到达C点后经过第四限的磁场后恰好被放在x轴上D点处（图上未画出）的一检测装置俘获，此后质子将不能再返回电场，则CD间的距离为多少．
如图所示，在直角坐标系xoy的第一、四象限区域内存在两个有界的匀强磁场：垂直纸面向外的匀强磁场I、垂直纸面向里的匀强磁场II，O、M、P、Q为磁场边界和x轴的交点OM=MP=L．在第三象限存在沿y轴正向的匀强电场．一质量为m、带电荷量为+q的粒子从电场中坐标为（-2L，-L）的点以速度υ0沿+x方向射出，恰好经过原点O处射入区域I又从M点射出区域I（粒子的重力忽略不计）．
（1）求第三象限匀强电场场强E的大小；
（2）求区域I内匀强磁场磁感应强度B的大小；
（3）如带电粒子能再次回到原点O，问区域II内磁场的宽度至少为多少？粒子两次经过原点O的时间间隔为多少？
在电子显像管内部，由炽热的灯丝发射出的电子在经过一定的电压加速后，进入偏转磁场区域，最后打到荧光屏上，当所加的偏转磁场的磁感应强度为零时，电子应沿直线运动打在荧光屏的正中心位置．但由于地磁场对带电粒子运动的影响，会出现在未加偏转磁场时电子束偏离直线运动的现象，所以在精密测量仪器的显像管中常需要在显像管的外部采取磁屏蔽措施以消除地磁场对电子运动的影响．
已知电子质量为m、电荷量为e，从炽热灯丝发射出的电子（可视为初速度为零）经过电压为U的电场加速后，沿水平方向由南向北运动．若不采取磁屏蔽措施，且已知地磁场磁感应强度的竖直向下分量的大小为B，地磁场对电子在加速过程中的影响可忽略不计．在未加偏转磁场的情况下，
（1）试判断电子束将偏向什么方向；
（2）求电子在地磁场中运动的加速度的大小；
（3）若加速电场边缘到荧光屏的距离为l，求在地磁场的作用下使到达荧光屏的电子在荧光屏上偏移的距离．
如图所示为某种质谱仪的工作原理示意图．此质谱仪由以下几部分构成：粒子源N；P、Q间的加速电场；静电分析器，即中心线半径为R的四分之一圆形通道，通道内有均匀辐射电场，方向沿径向指向圆心O，且与圆心O等距的各点电场强度大小相等；磁感应强度为B的有界匀强磁场，方向垂直纸面向外；胶片M．由粒子源发出的不同带电粒子，经加速电场加速后进入静电分析器，某些粒子能沿中心线通过静电分析器并经小孔S垂直磁场边界进入磁场，最终打到胶片上的某点．粒子从粒子源发出时的初速度不同，不计粒子所受重力．下列说法中正确的是（　　）
A．从小孔S进入磁场的粒子速度大小一定相等
B．从小孔S进入磁场的粒子动能一定相等
C．打到胶片上同一点的粒子速度大小一定相等
D．打到胶片上位置距离O点越远的粒子，比荷越大

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网