Question

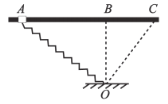
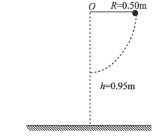
【题目】如图所示，一质量m=1.0kg的小球系在竖直平面内长度R=0.50m的轻质不可伸长的细线上，O点距水平地面的高度h=0.95m。让小球从图示水平位置由静止释放，到达最低点的速度v=3.0m/s，此时细线突然断开。取重力加速度g=10m/s2.求：

(1)小球落地点与O点的水平距离x。

(2)小球在摆动过程中，克服阻力所做的功W；

(3)细线断开前瞬间小球对绳子的拉力T。

Answer 1

【答案】(1)0.9m；(2)0.5J；(3)28N，方向竖直向下

【解析】

(1)小球从最低点出发做平抛运动，根据平抛运动的规律得
水平方向

x=vt

竖直方向

解得

x=0.9m

(2)小球摆下的过程中，根据动能定理得

解得

(3)小球在圆最低点受重力和拉力，根据牛顿第二定律得

解得

FT=28N

根据牛顿第三定律可知，球对绳拉力大小为28N，方向竖直向下。