��Ŀ����
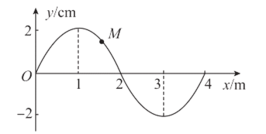
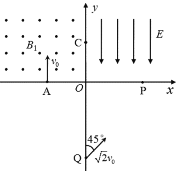
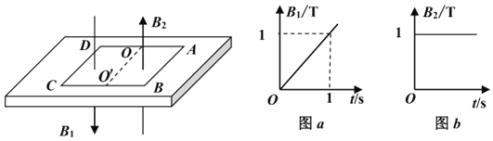
����Ŀ����ͼ��ʾΪ�������г�ģ�ͣ�����M=2kg�ľ�Ե�������ֹ�ڶ�Ħ��������1=0.1�Ĵֲ�ˮƽ�����ϡ�λ�ڴų��е������ν�����ABCDΪ����Դ��������m��2kg���߳�Ϊ1m������Ϊ![]() �����Ե���Ķ�Ħ��������2=0.2��
�����Ե���Ķ�Ħ��������2=0.2��![]() ΪAD��BC���е㡣�ڽ��������п��������ͬ���ƶ��Ĵų���
ΪAD��BC���е㡣�ڽ��������п��������ͬ���ƶ��Ĵų���![]() �����ڴų���ͼa��ʾ��CDǡ�ڴų���Ե���⣻
�����ڴų���ͼa��ʾ��CDǡ�ڴų���Ե���⣻![]() �����ڴų���ͼb��ʾ��ABǡ�ڴų���Ե���ڣ�g=10m/s2��������Ե���㹻������Ϊ��Ե�����������Ħ�������ڻ���Ħ�������������Ӿ�ֹ�ͷź� ��
�����ڴų���ͼb��ʾ��ABǡ�ڴų���Ե���ڣ�g=10m/s2��������Ե���㹻������Ϊ��Ե�����������Ħ�������ڻ���Ħ�������������Ӿ�ֹ�ͷź� ��
A.��������̶��ھ�Ե���ϣ�������ļ��ٶ�Ϊ2m/s2
B.��������̶��ھ�Ե���ϣ�������ļ��ٶ�Ϊ1m/s2
C.�������̶���������ļ��ٶ�Ϊ6m/s2����Ե��ļ��ٶ�Ϊ1m/s2
D.�������̶���������ļ��ٶ�Ϊ2m/s2����Ե���Ծ�ֹ
���𰸡�BD
��������
AB����������̶��ھ�Ե���ϣ�![]() ����ų��仯��������Ӧ�綯�ƣ����ݷ����ڵ�Ÿ�Ӧ������
����ų��仯��������Ӧ�綯�ƣ����ݷ����ڵ�Ÿ�Ӧ������
E=![]() =0.5V
=0.5V
����ŷķ���ɿ�֪����·�еĵ���Ϊ
I=![]() =8A
=8A
AB���ܵ�����������
F=BIL=8N
����ţ�ٵڶ�������
![]()
![]()
�������ݽ��a=1m/s2����A����B��ȷ��
CD���������̶��ھ�Ե���ϣ��Խ�������ţ�ٵڶ����ɣ�����
![]()
���a��=2m/s2
�Ծ�Ե�壬��ţ�ٵڶ����ɣ�����
![]()
��ã�a��=0���������ļ��ٶ�Ϊ2m/s2����Ե���Ծ�ֹ����C����D��ȷ��
��ѡBD��

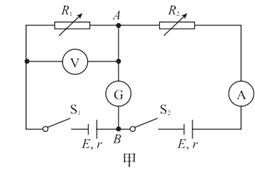
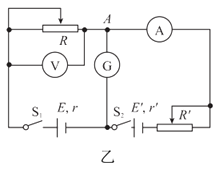
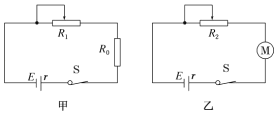
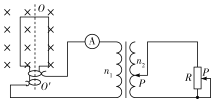
����Ŀ�����������IJ����������ĵ��ݣ�һ����õ����һֱ̨����ѹ��Դ��һ����������������ѹ16V������ֵ����R1����ֵδ֪������ֵ����R2=150�������������������ݲɼ����ͼ����������˫������S���������ɣ�
ʵ��������£�
ʵ����� | ʵ�鲽�� |
��1�� | ���ö��õ��������10������������R1��ָ��ƫת��ͼ����ʾ�� |
�ڽ�����R1�����İ���ͼ����ȷ���ӵ�·��������S��1�����ӣ���Դ���������磮 | |
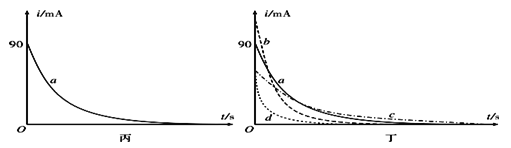
�۽�����S����2�ˣ���õ�����ʱ��仯��i��t������ͼ���е�ʵ��a��ʾ�� | |
��2�� | ���õ���R2�滻R1���ظ�����ʵ�鲽��ڢۣ���õ�����ʱ��仯��i��t������ͼ���е�ij��������ʾ�� |
˵��������ʵ���е�Դ�����ֱ����ѹ�㶨����ͬ�� | |
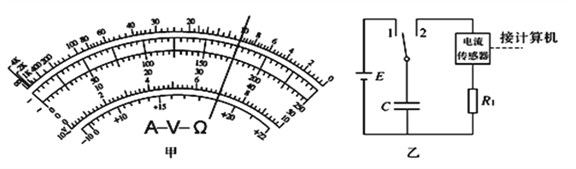
������������⣺
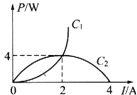
��1����ͼ��֪������R1�IJ���ֵΪ______����
��2����1��ʵ���У�����R1���˵�����ѹU=___V�����ü�����������i��t���ߺ�����������Χ�����Ϊ42.3mAS����֪�������ŵ�ʱ��������Ժ��Բ��ƣ���������ĵ���ΪC=________��
��3����2��ʵ���У�������ʱ��仯��i��t����Ӧ����ͼ���е�����__��ѡ����b������c������d�������ж�������_________________________________________________��