题目内容
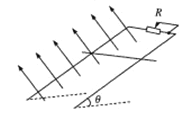
【题目】如图所示，足够长的光滑平行金属导轨与水平面的夹角为θ，导轨上端接有可变电阻R装置所在空间存在垂直于导轨平面向上的匀强磁场，磁感应强度大小为B。现有一根质量为m的金属棒在金属导轨上从同一位置由静止滑下，金属棒的有效电阻为r，导轨电阻可忽略不计，金属棒始终与导轨垂直且接触良好，经过一段时间，金属棒下滑距离为x时其速度恰好达到最大值vm，则下列说法正确的是
A. 电阻R一定时，金属棒达到最大速度对应的最大动能与此时回路总的电功率成正比
B. vm=
C. 电动势最大值Em与电阻R成正比
D. 金属棒达到最大速度后，减少的机械能全部转化为电热能
【答案】ABD
【解析】
导体棒最终匀速运动受力平衡可求最大速度，由牛顿第二定律结合安培力的表达式求加速度，由能量守恒推断能之间的相互转化．
B、棒在重力的分力和逐渐增大的安培阻力作用下先做加速度减小的变加速直线运动，后做匀速直线运动，有
，可得
；故B正确.
C、最大动生电动势为
，可见Em与电阻R成线性函数但不是正比例函数；故C错误.
A、金属棒达到最大速度对应的最大动能为
，回路的电功率为
，则
，即电阻R一定时，最大动能与总的电功率成正比；故A正确.
D、对棒由动能定理
，当棒匀速运动时
，即减少的重力势能全部变成电能转化为热能；故D正确.
故选ABD.
练习册系列答案
阅读快车系列答案
相关题目
