题目内容
【题目】如图所示,在坐标系xOy内有一半径为a的圆形区域,圆心坐标为O1(a,0),圆内分布有垂直纸面向里的匀强磁场,在直线y=a的上方和直线x=2a的左侧区域内,有一沿x轴负方向的匀强电场,场强大小为E,一质量为m、电荷量为+q(q>0)的粒子以速度v从O点垂直于磁场方向射入,当入射速度方向沿x轴方向时,粒子恰好从O1点正上方的A点射出磁场,不计粒子重力,求:
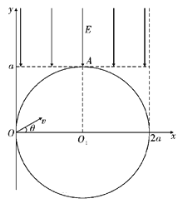
(1)磁感应强度B的大小;
(2)粒子离开第一象限时速度方向与y轴正方向的夹角正切值;
(3)若将电场方向变为沿y轴负方向,电场强度大小不变,粒子以速度v从O点垂直于磁场方向、并与x轴正方向夹角θ=300射入第一象限,求粒子从射入磁场到最终离开磁场的总时间t
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据几何关系先得到圆心、半径,再根据洛伦兹力提供向心力列式求解;
(2)粒子离开磁场后,进入电场,根据动能定理列式求解粒子在电场中的位移;粒子进入电场到达最高点后,又沿原路返回磁场,再得到第二次圆心和射出点,最后得到总路程;
(3)粒子在磁场中做圆周运动,先得到第一次圆心和射出点,进入电场后,又沿原路返回,再得到第二次圆心和射出点,最后得到总时间.
(1)当粒子速度沿x轴方向入射,从A点射出磁场时,几何关系知:r=a
由![]()
![]()
(2)从A点进入电场后作类平抛运动;
沿水平方向做匀加速直线运动:![]()
沿竖直方向做匀速直线运动:vy=v0
∴粒子离开第一象限时速度与y轴的夹角:![]()
(3)粒子从磁场中的P点射出,因磁场圆和粒子的轨迹圆的半径相等,OO1PO2构成菱形,故粒子从P点的出射方向与OO1平行,即与y轴平行;轨迹如图所示:
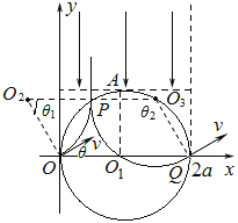
∴粒子从O到P所对应的圆心角为θ1=60°,粒子从O到P用时:![]()
由几何知识可知,粒子由P点到x轴的距离![]()
粒子在电场中做匀变速运动的时间:![]()
粒子磁场和电场之间匀速直线运动的时间:![]()
粒子由P点第2次进入磁场,从Q点射出,PO1QO3构成菱形;由几何知识可知Q点在x轴上,即为(2a,0)点;
粒子由P到Q所对应的圆心角θ2=120°,粒子从P到Q用时:![]()
∴粒子从射入磁场到最终离开磁场的总时间:![]()

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】光电管是一种利用光照射产生电流的装置,当入射光照在管中金属板上时,可能形成光电流。表中给出了6次实验的结果。
组 | 次 | 入射光子的能量/eV | 相对光强 | 光电流大小/mA | 逸出光电子的最大动能/eV |
第 一 组 | 1 2 3 | 4.0 4.0 4.0 | 弱 中 强 | 29 43 60 | 0.9 0.9 0.9 |
第 二 组 | 4 5 6 | 6.0 6.0 6.0 | 弱 中 强 | 27 40 55 | 2.9 2.9 2.9 |
由表中数据得出的论断中不正确的是
A. 两组实验采用了不同频率的入射光
B. 两组实验所用的金属板材质不同
C. 若入射光子的能量为5.0 eV,逸出光电子的最大动能为1.9 eV
D. 若入射光子的能量为5.0 eV,相对光强越强,光电流越大