Question

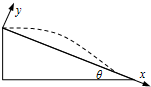
在倾角为θ的斜面上O点以初速度v₀平抛一小球，小球落在斜面上A点．求：
（1）小球从O飞到A点的时间及O、A两点间的距离．
（2）从抛出开始经多长时间离斜面最远？最远距离为多少？

Answer 1

（1）小球做平抛运动，在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，由题有：

1 2 gt2

v0t

=tanθ
解得：t=

2v0tanθ

g

水平位移为：x=v₀t=

2 v 20 tanθ

g

则O、A两点间的距离为：S=

x

cosθ

=

2 v 20 tanθ

gcosθ

（2）采用正交分解法，将该运动分解在沿斜面和垂直于斜面两个方向上，那么在x方向物体做匀加速直线运动，在y方向物体做匀减速直线运动，有：v_0x=v₀cosθ，v_0y=v₀sinθ，
a_x=gsinθ a_y=gcosθ
当v_y=0时物体离斜面最远，有：v₀sinθ-a_yt₁=0
故有：t=

v0tanθ

g

设最远距离为h，则有：

v

20y

=2a_yh
所以解得：h=

v 20

g

sinθtanθ．
答：（1）小球从O飞到A点的时间为

2 v 20 tanθ

g

，O、A两点间的距离为

2 v 20 tanθ

gcosθ

．
（2）从抛出开始经

v0tanθ

g

时间离斜面最远，最远距离为

v 20

g

sinθtanθ．