题目内容
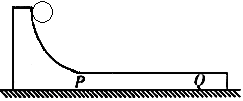
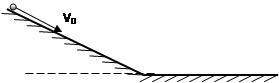
如图所示，质量为M，半径为R的四分之一圆弧状木块，放在光滑的水平面，其中PQ段水平，P点是圆弧最低点。一个质量为m的小球从最高点开始自由滑下，不考虑一切摩擦，以下结论正确的是（ ）
A．小球达到P点时，小球的速度为 |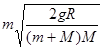
| B．小球达到P点时，木块的速度为 |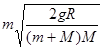
| C．在到达P点瞬间小球对木块的压力大于mg |
| D．在到达P点瞬间小球对木块的压力等于mg |
BC
本题主要考查牛顿第二定律、动量守恒和机械能守恒定律的条件，需要注意的是滑块从最高点到P的过程中，系统动量不守恒，但在水平方向上动量守恒，因为系统在水平方向上没有受到外作作用。解题时还需注意到达P点瞬间小球有向心加速度，所受合外力不为零。
小球从最高点下滑到P的过程中，系统在水平方向上动量守恒、机械能守恒，令小球到达P点时的速度为
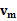，木块的的速度
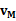，则：由水平方向动量守恒得mvm+MvM=0 （1）
由机械能守恒定律可得
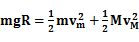（2）由方程（1）、（2）解得：
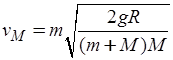
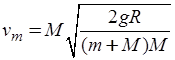
故A错误，B正确；小球到达P点瞬间具有向心加速度，所受合力不为零，由牛顿第二定律知小球受到的支持力
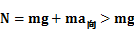，由牛顿第三定律知小球对木块的压力
，故C正确，D错误。所以选BC。
练习册系列答案
相关题目
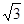/2