题目内容
18.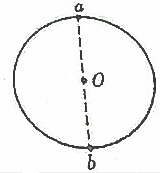 如图所示,半径为R的一个飞轮的圆心在O,但它的重心不在转轴O处(转轴通过圆心O),工人师傅在飞轮边缘上的a处挖下一小块质量为△m的金属加固到正对面的轮边缘的b处,这时飞轮的重心位置正好在O处,现由于b处加固的△m这块金属已脱落丢失,又使得飞轮的重心不在O处,工人师傅决定再在a处挖去一小块质量的金属,不用加固到b处,这样也能将飞轮的重心调到O处,问再挖去的一小块金属的质量等于多少?
如图所示,半径为R的一个飞轮的圆心在O,但它的重心不在转轴O处(转轴通过圆心O),工人师傅在飞轮边缘上的a处挖下一小块质量为△m的金属加固到正对面的轮边缘的b处,这时飞轮的重心位置正好在O处,现由于b处加固的△m这块金属已脱落丢失,又使得飞轮的重心不在O处,工人师傅决定再在a处挖去一小块质量的金属,不用加固到b处,这样也能将飞轮的重心调到O处,问再挖去的一小块金属的质量等于多少?
分析 当质量分布均匀,形状规则时,物体的重心在其几何中心,根据b处加固的△m没有脱落时,飞轮的重心在O点可知,此时飞轮质量“分布均匀,形状规则”了,若b处脱落质量为△m的金属块,要使中心还在O处,则要在a处再挖去一小块质量为△m的金属块.
解答 解:b处加固的△m没有脱落时,飞轮的重心在O点,设想在ab两处都拿走了△m的质量,由于ab两处相对圆心O对称,因而飞轮的重心仍在O处,由此可知,在b处脱落质量为△m的金属块后,只要在a处再挖去一小块质量为△m的金属块即可.
答:再挖去的一小块金属的质量等于△m.
点评 本题主要考查了重心位置的影响因素,知道当质量分布均匀,形状规则时,物体的重心在其几何中心,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.有一些关于运动学的概念和计算,其中正确的是( )
| A. | 为了简捷的研究物理问题,物理学引入了质点模型,质点实际上也存在 | |
| B. | 在本届秋季运动会4×100m的接力赛中,一(1)队取得了45.45s的好成绩,4位运动员的奔跑的平均速度约为8.8/s | |
| C. | 物体做匀变速直线运动,其加速度大小3m/s2,表示物体在任何1s内速度都增加3m/s | |
| D. | 一般讲平均速度时,必须讲清楚是哪段时间(或哪段位移)内的平均速度 |
3.下列关于重力加速度的说法正确的是( )
| A. | 重力加速度g是标量,只有大小,没有方向 | |
| B. | 在地球上不同地方,g的大小是不同的,但差别不大 | |
| C. | 在地球上同一地点,轻石块与重石块做自由运动的加速度是相同的 | |
| D. | 纬度越低的地方,重力加速度g值越小 |
15.已知地球和火星绕太阳公转的轨道半径分别为R1和R2(公转轨迹近似为圆),如果把行星与太阳连线扫过的面积与其所用时间的比值定义为扫过的面积速率.则地球和火星绕太阳公转过程中扫过的面积速率之比是( )
| A. | $\frac{{R}_{1}}{{R}_{2}}$ | B. | $\frac{\sqrt{{R}_{1}}}{\sqrt{{R}_{2}}}$ | C. | $\frac{{R}_{2}}{{R}_{1}}$ | D. | $\frac{\sqrt{{R}_{2}}}{\sqrt{{R}_{1}}}$ |

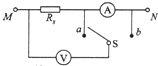 如图所示,用伏安法测电阻Rx时,MN接在恒定电压上,当S接a点时电压表示数为10V,电流表示数为0.2A;当S接b点时,电压表示数为12V,电流表示数为0.15A.求:
如图所示,用伏安法测电阻Rx时,MN接在恒定电压上,当S接a点时电压表示数为10V,电流表示数为0.2A;当S接b点时,电压表示数为12V,电流表示数为0.15A.求: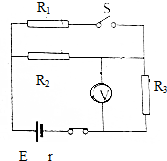 在如图电路中,电阻R1=R2=R3=1Ω,当S闭合时,电压表示数为1V,当S断开时,电压表示数为0.8V,试求电路中电源的电动势和内阻.
在如图电路中,电阻R1=R2=R3=1Ω,当S闭合时,电压表示数为1V,当S断开时,电压表示数为0.8V,试求电路中电源的电动势和内阻.