题目内容
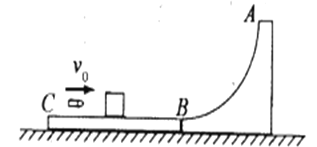
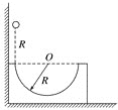
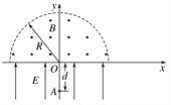
【题目】如图所示,x轴上方以原点O为圆心、半径为R=2 m的半圆形区域内存在匀强磁场,磁场的方向垂直于xOy平面向外,磁感应强度为B=![]() T。在x轴下方的区域内存在方向与y轴相同的匀强电场。y轴下方的A点与O点的距离为d=1 m,一质量为m=2
T。在x轴下方的区域内存在方向与y轴相同的匀强电场。y轴下方的A点与O点的距离为d=1 m,一质量为m=2![]() kg、电荷量为q=2 C的带正电粒子从A点由静止释放,经电场加速后从O点射入磁场,不计粒子的重力作用。
kg、电荷量为q=2 C的带正电粒子从A点由静止释放,经电场加速后从O点射入磁场,不计粒子的重力作用。
(1)要使粒子进入磁场之后不再经过x轴,电场强度需大于或等于某个值E,求E;
(2)若电场强度变化为第(1)问中电场强度E的![]() ,求粒子经过磁场偏转后到达x轴时的坐标,并求粒子从A点出发到该位置的时间。
,求粒子经过磁场偏转后到达x轴时的坐标,并求粒子从A点出发到该位置的时间。
【答案】(1)![]() V/m;(2)(
V/m;(2)(![]() ,0),(2
,0),(2![]() +
+![]() ) s。
) s。
【解析】
(1)粒子在电场中做匀加速运动,由动能定理得:
qEd=![]() mv2
mv2
粒子在磁场中做匀速圆周运动,由牛顿第二定律得:
![]()
粒子恰好不经过x轴,则离开磁场时速度方向与x轴平行,作出粒子运动轨迹如图所示:
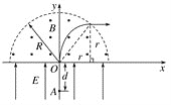
由几何关系得:
R=![]() r
r
联立方程解得:E=![]() =
=![]() V/m;
V/m;
(2)由E′=![]() E得,E′=
E得,E′=![]() ,可知:
,可知:
r=![]()
作出粒子运动轨迹如图所示:
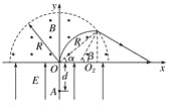
由:
cosα=![]() =
=![]()
得:α=30°,所以:
β=2α=60°
粒子经x轴时位置坐标为:
x=r+![]()
解得:x=![]() R=2
R=2![]() m,坐标为:(2
m,坐标为:(2![]() m,0);
m,0);
粒子在电场中:由
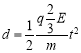
得:t1=![]() =
=![]() ,v=
,v=![]() t1
t1
粒子在磁场中:
t2=![]() ·
·![]() =
=![]() πs
πs
出磁场后运动到x轴的时间:t3=![]() =
=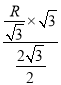 =
=![]() ;
;
综上,粒子从A点出发到该位置的时间:
t=t1+t2+t3=(2![]() +
+![]() ) s。
) s。

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】要测绘额定电压为2 V的小灯泡的伏安特性曲线,所供选择的器材除了导线和开关外,还有以下一些器材可供选择:
A.电源E(电动势3.0 V,内阻不计)
B.电压表V1(量程0~3.0 V,内阻约2 kΩ)
C.电压表V2(量程0~15.0 V,内阻约6 kΩ)
D.电流表A1(量程0~0.6 A,内阻约1 Ω)
E.电流表A2(量程0~100 mA,内阻约2 Ω)
F.滑动变阻器R1(最大阻值10 Ω)
G.滑动变阻器R2(最大阻值2 kΩ)
(1)为了减小实验误差,实验中电压表应选择________,电流表应选择_______,滑动变阻器应选择_________________。(填写各器材的序号)
(2)为提高实验精度,请你设计实验电路图,并画在下面的虚线框中。
(_______)

(3)实验中测得一组数据如下表所示,根据表格中的数据在图中坐标系中作出小灯泡的伏安特性曲线。
I/A | 0 | 0.12 | 0.21 | 0.29 | 0.34 | 0.38 | 0.42 | 0.45 | 0.47 | 0.49 | 0.50 |
U/V | 0 | 0.20 | 0.40 | 0.6 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 | 2.00 |
(_______)
(4)该小灯泡的额定功率是_________ W。(保留两位小数)
(5)由图象可知,小灯泡电阻的变化特点是_________________。
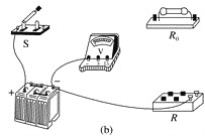
【题目】用电流表和电压表测定2节干电池串联组成的电池组的电动势和内电阻。要求尽量减小实验误差。
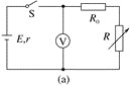
(1)实验电路应该选择下图中的________(选填“甲”或“乙”)。
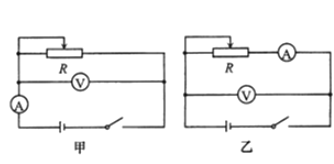
(2)现有电压表(![]() )、开关和导线若干,以及以下器材:
)、开关和导线若干,以及以下器材:
A.电流表(![]() )
)
B.电流表(![]() )
)
C.滑动变阻器(![]() )
)
D.滑动变阻器(![]() )
)
实验中电流表应选用___________;滑动变阻器应选用____________。(选填相应器材前的字母)
(3)某位同学记录的6组数据如下表所示,请在![]() 坐标系上标出6组数据的对应点,画出
坐标系上标出6组数据的对应点,画出![]() 图线____________________________________。
图线____________________________________。
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
电压 | 2.80 | 2.50 | 2.20 | 1.90 | 1.60 | 1.30 |
电流 | 0.12 | 0.32 | 0.50 | 0.68 | 0.88 | 1.06 |
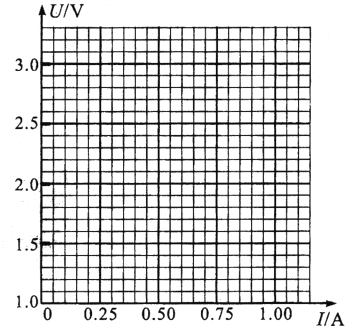
(4)根据(3)中所画图线可得出电池组的电动势![]() ___________
___________![]() ,内电阻
,内电阻![]() _______
_______![]() 。
。