题目内容
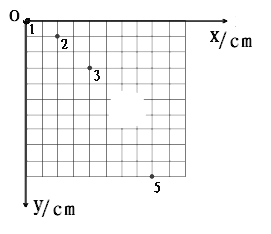
【题目】如图所示，有一个可视为质点的质量为m=1kg的小物块，从光滑平台上的A点以v0=1.8m/s的初速度水平抛出，到达C点时，恰好沿C点的切线方向进人固定在竖直平面内的光滑圆弧轨道，最后小物块无碰撞地滑上紧靠轨道末端D点的足够长的水平传送带．已知传送带上表面与圆弧轨道末端切线相平，传送带沿顺时针方向匀速运行的速度为v=3m/s，小物块与传送带间的动摩擦因数μ=0.5，圆弧轨道的半径为R=2m，C点和圆弧的圆心O点连线与竖直方向的夹角θ=53°，不计空气阻力，重力加速度g=10m/s2，sin53°=0.8，cos53°=0.6．求：
（1）小物块达到C点时的速度；
（2）小物块到达圆弧轨道末端D点时对轨道的压力；
（3）小物块从滑上传送带到第一次离开传送带的过程中产生的热量
【答案】（1）3m/s（2）22.5N，方向竖直向下（3）32J
【解析】
（1）设物块在C点的速度为vC，在C点由vC=
，解得小物块达到C点时的速度vC=3m/s
（2）设在D点的速度为vD，从C到D由动能定理得：mgR(1-
)=
mvD2-mvC2
解得：vD=5m/s
在D点设轨道对小球的作用力为FN：FN-mg=m
，解得：FN=22.5N，由牛顿第三定律知物块对轨道的压力大小为22.5N，方向竖直向下。
（3）设物块在传送带上加速度为a：
，a=
=5m/s2
物块由D点向左减速至速度为零所用时间t1，向左运动的位移x1，则有：vD=at1，x1=
t1， t1时间内传送带向右的位移为x2=vt1
物块速度由零增加到与传送带向右速度相等过程所用时间t2，t2=
，物块在t2时间内向右通过的位移x3，x3=
t2
传送带在t2时间内向右的位移为x4=vt2
小木块相对传送带移动的位移为：
x=x1+x2+x4-x3，
小物块从滑上传送带到第一次离开传送带的过程中产生的热量：Q=
x，解得Q=32J
