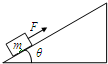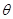题目内容
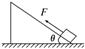
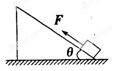
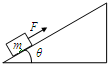 如图所示,一物体m在沿斜面向上的恒力F作用下,由静止从底端沿光滑的斜面向上做匀加速直线运动,经时间t力F做功为60J,此后撤出力F,物体又经过时间t回到出发点,若以地面为零势能面,则下列说法正确的是( )
如图所示,一物体m在沿斜面向上的恒力F作用下,由静止从底端沿光滑的斜面向上做匀加速直线运动,经时间t力F做功为60J,此后撤出力F,物体又经过时间t回到出发点,若以地面为零势能面,则下列说法正确的是( )分析:求物体回到出发点的动能可以运用动能定理,抓住整个过程中重力做功为零.撤去F前,物体做匀加速运动,撤去后做匀减速运动,两个过程的位移大小相等、方向相反,用平均速度表示位移,列式可求出撤去F瞬时与回到出发点瞬时速度关系,再分两个过程,根据动量定理可求出F的大小.根据动能定理求解撤出力F时物体的重力势能.根据撤去F时动能与重力势能的大小关系,分析两者相等的位置.
解答:解:A、对于整个过程,由动能定理得:Ek=WF=60J,所以物体回到出发点的动能为60J.故A正确.
B、取沿斜面向上方向为正方向,撤去F时物体速度大小为v,回到出发点时速度大小为v′.撤去F前,物体做匀加速运动,撤去后做匀减速运动,两个过程的位移大小相等、方向相反,则有
t=-
t,则得v′=2v,
根据动量定理得:
匀加速运动过程,有Ft-mgsinθt=mv
匀减速运动过程,有-mgsinθt=-mv′-mv
解得,F=
mgsinθ.故B错误.
C、由上知,物体回到出发点时的动能Ek′=
mv′2=60J,刚撤去F时,Ek=
mv2=
m(
)2=
Ek=15J
对于匀加速运动,由动能定理得:WF-mgh=Ek.则得mgh=WF-Ek=60J-45J=45J,即撤出力F时,物体的重力势能是45J,故C正确.
D、由上看出,撤去F前,由动量定理得,(F-mgsinθ)t=mvt,解得vt=
gsinθt,t时刻动能为EKt=
m
=
mg2sin2θt2
重力势能EP=mg
tsinθ=
mg2sin2θt2,可见,动能总小于重力势能,而撤去F后,在下滑过程中,动能增大,重力势能减小到零,所以动能与重力势能会相等,故D正确.
故选ACD
B、取沿斜面向上方向为正方向,撤去F时物体速度大小为v,回到出发点时速度大小为v′.撤去F前,物体做匀加速运动,撤去后做匀减速运动,两个过程的位移大小相等、方向相反,则有
| v |
| 2 |
| v-v′ |
| 2 |
根据动量定理得:
匀加速运动过程,有Ft-mgsinθt=mv
匀减速运动过程,有-mgsinθt=-mv′-mv
解得,F=
| 4 |
| 3 |
C、由上知,物体回到出发点时的动能Ek′=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| v |
| 2 |
| 1 |
| 4 |
对于匀加速运动,由动能定理得:WF-mgh=Ek.则得mgh=WF-Ek=60J-45J=45J,即撤出力F时,物体的重力势能是45J,故C正确.
D、由上看出,撤去F前,由动量定理得,(F-mgsinθ)t=mvt,解得vt=
| 1 |
| 3 |
| 1 |
| 2 |
| v | 2 t |
| 1 |
| 18 |
重力势能EP=mg
| v |
| 2 |
| 1 |
| 6 |
故选ACD
点评:本题考查的知识点较多,要善于选择研究的过程,根据位移关系,由运动学公式求出速度关系是关键.

练习册系列答案
相关题目
如图所示,一物体m在沿斜面向上的恒力F作用下,由静止从底端沿光滑的斜面向上做匀加速直线运动,经时间t力F做功为60 J,此后撤去恒力F,物体又经时间t回到出发点,若以地面为零势能点,则下列说法正确的是 ( )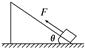
| A.物体回到出发点时的动能是60 J |
| B.开始时物体所受的恒力F=2mgsinθ |
| C.撤去力F时,物体的重力势能是45 J |
| D.动能与势能相同的位置在撤去力F之前的某位置 |