Question

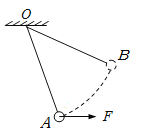
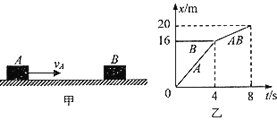
【题目】如图所示，一质量为6m、长L=0.80m的薄木板AB放在光滑的水平平台上，木板B端与台面右边缘齐平．B端上放有质量为3m且可视为质点的滑块C，C与木板之间的动摩擦因数为．质量为m的小球也用长为L的细绳悬挂在平台右边缘正上方的O点，细绳竖直时小球恰好与滑块C接触．现将小球向右拉至细绳水平并由静止释放，在最低点与滑块C发生弹性正碰．（g=10m/s2）

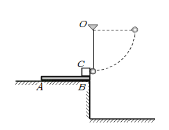
（1）求小球与滑块C碰后能上的最大高度h；

（2）通过计算判断C能否从木板上掉下来?

Answer 1

【答案】（1）h=0.2 m（2）滑块C不会从木板上掉下来

【解析】

（1）设小球运动到最低点的速率为v0，小球向下摆动过程机械能守恒，由机械能守恒定律得

解得

以小球的初速度方向为正方向, 对小球与C组成的系统，由动量守恒得; 由能量守恒得：

解得

小球与C碰后机械能守恒有 即上升最大高度h=0.2 m

（2）假设木板足够长，在C与木板相对滑动S直到相对静止过程，设两者最终共同速率为 v3，以C的初速度方向为正方向，由动量守恒定律得 由能量守恒定律得

代入数据得

由S＜L知，滑块C不会从木板上掉下来