题目内容
【题目】将以下正确命题的序号填写在横线上___________.
①若![]() ,
,![]() ,且
,且![]() 与
与![]() 夹角为锐角,则
夹角为锐角,则![]() ;
;
②点O是三角形ABC所在平面内一点,且满足![]() ,则点O是三角形ABC的重心;
,则点O是三角形ABC的重心;
③若ΔABC中,![]() ,则ΔABC是钝角三角形;
,则ΔABC是钝角三角形;
④若![]() ,则点P为ABC的内心.
,则点P为ABC的内心.
【答案】③④
【解析】
①根据向量夹角与数量积之间的关系即可判断;
②根据三角形重心性质即可判断;
③根据向量夹角与数量积之间的关系即可判断;
④根据三角形内心性质即可判断.
①若![]() 与
与![]() 夹角为锐角,则
夹角为锐角,则![]() 且
且![]() 与
与![]() 不共线,即
不共线,即![]() ,即
,即![]() 且
且![]() ,故①不正确;
,故①不正确;
②由![]() 得,
得,![]() 即
即![]() ,同理可得,
,同理可得,![]() ,所以点O是三角形ABC的垂心,故②不正确;
,所以点O是三角形ABC的垂心,故②不正确;
③![]() 即
即![]() ,所以
,所以![]() ,即角
,即角![]() 为钝角,所以ΔABC是钝角三角形,正确;
为钝角,所以ΔABC是钝角三角形,正确;
④因为![]() ,所以
,所以![]() ,
,
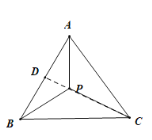
如图所示,在![]() 中,延长
中,延长![]() 交
交![]() 于
于![]() ,
,
设![]() ,
,![]() ,由
,由![]() ,所以有
,所以有
![]() ,即
,即![]() ,
,
因为![]() 不共线,所以
不共线,所以![]() ,即
,即![]() ,因此
,因此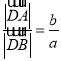 ,由角平分线定理的逆定理可知,
,由角平分线定理的逆定理可知,![]() 为
为![]() 的平分线,同理可知,
的平分线,同理可知,![]() 为
为![]() 的平分线,故点P为ABC的内心,正确.
的平分线,故点P为ABC的内心,正确.
故答案为:③④.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目