题目内容
如图甲所示,竖直平面内的光滑轨道由倾斜直轨道AB和圆轨道BCD组成,AB和BCD相切于B点,CD连线是圆轨道竖直方向的直径(C、D为圆轨道的最低点和最高点),已知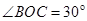 。可视为质点的小滑块从轨道AB上高H处的某点由静止滑下,用力传感器测出滑块经过圆轨道最高点D时对轨道的压力为F,并得到如图乙所示的压力F与高度H的关系图象,取
。可视为质点的小滑块从轨道AB上高H处的某点由静止滑下,用力传感器测出滑块经过圆轨道最高点D时对轨道的压力为F,并得到如图乙所示的压力F与高度H的关系图象,取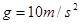 。求:
。求:
(1)滑块的质量和圆轨道的半径;
(2)是否存在某个H值,使得滑块经过最高点D后能直接落到直轨道AB上与圆心等高的点。若存在,请求出H值;若不存在,请说明理由。
(1)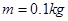 ,
,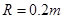 (2)
(2)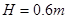
解析试题分析:(1)小滑块从A到D的过程,由动能定理得:
在D点由牛顿第二定律有: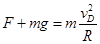
解得:
取点(0.50m,0)和(1.00m,5.0N)代入上式得: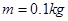 ,
,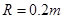 。
。
(2)假设滑块经过最高点D后能直接落到直轨道AB上与圆心等高的E点(如下图所示)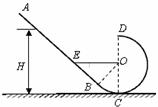
设在D点速度为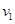 ,有:
,有: ,
, ,得到:
,得到: 。
。
当滑块在D点时,轨道对其压力为0有最小速度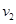 ,有:
,有: ,得:
,得: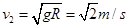
由于 ,所以H存在,从A到D的过程,由动能定理得:
,所以H存在,从A到D的过程,由动能定理得:
解得: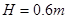
考点:本题考查了动能定理、圆周运动、平抛运动。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
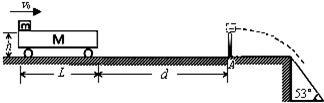

 。在水平桌面上画等距的三条平行于桌子边缘的直线1、2、3,如图所示。空气和桌面对物体的阻力均忽略不计。
。在水平桌面上画等距的三条平行于桌子边缘的直线1、2、3,如图所示。空气和桌面对物体的阻力均忽略不计。
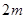 的木板A静止在光滑水平面上,其右端与固定挡板相距
的木板A静止在光滑水平面上,其右端与固定挡板相距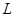 ,内壁光滑的弹射器利用压缩弹簧把质量为
,内壁光滑的弹射器利用压缩弹簧把质量为 的物块B(视为质点)水平向右弹射出去,B弹出后从A左端的上表面水平滑入,之后立刻拿走弹射器。已知A足够长,B不会从A表面滑出,A与挡板的碰撞无机械能损失;弹射器弹簧储存的弹性势能为
的物块B(视为质点)水平向右弹射出去,B弹出后从A左端的上表面水平滑入,之后立刻拿走弹射器。已知A足够长,B不会从A表面滑出,A与挡板的碰撞无机械能损失;弹射器弹簧储存的弹性势能为 ,重力加速度为
,重力加速度为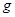 ,不计空气阻力。
,不计空气阻力。


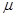 满足的条件。
满足的条件。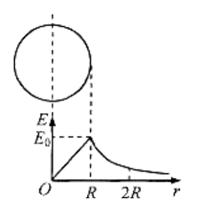
 的电场加速后,从C点沿水平方向飞入电场强度为
的电场加速后,从C点沿水平方向飞入电场强度为 的匀强电场中,到达该电场中另一点D时,电子的速度方向与电场强度方向的夹角正好是120°,如图所示。试求C、D两点沿电场强度方向的距离y。
的匀强电场中,到达该电场中另一点D时,电子的速度方向与电场强度方向的夹角正好是120°,如图所示。试求C、D两点沿电场强度方向的距离y。

