题目内容
（12分）半径为R，均匀带正电荷的球体在空间产生球对称的电场；场强大小沿半径分布如图所示，图中E0已知，E－r曲线下O－R部分的面积等于R－2R部分的面积。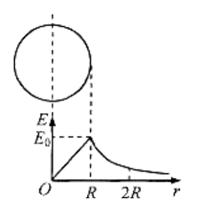
（1）写出E－r曲线下面积的单位；
（2）已知带电球在r≥R处的场强E=kQ／r2，式中k为静电力常量，该均匀带电球所带的电荷量Q为多大?
（3）求球心与球表面间的电势差△U；
（4）质量为m，电荷量为q的负电荷在球面处需具有多大的速度可以刚好运动到2R处?
（1）V（伏特）（2）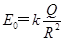
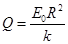（3）
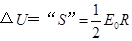
（4）
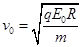
解析试题分析： （1）根据关系式U=Ed可知，E－r曲线下面积表示电势差，其单位是V（伏特）。
（2）将r=R，E=E0代入关系式E=kQ／r2可得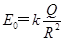，所以。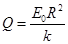
（3）根据（1）可知，球心与球表面间的电势差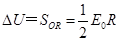
（4）由动能定理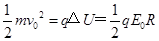
可得，.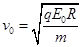
考点：本题考查应用图象分析问题的能力、动能定理。
练习册系列答案
相关题目
后脱离墙面，此时速度大小为
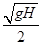，最终落在地面。
d，右端为屏，屏足够大与极板垂直，到极板右端的距离为D。有一细电子束沿图中虚线以速度v0连续不断地射入电场且能穿出。已知电子电量为e，电子质量为m,平行板电容器极板间可调偏转电压为UMN，忽略细电子束的宽度及电子所受的重力及电子间的相互作用力。求：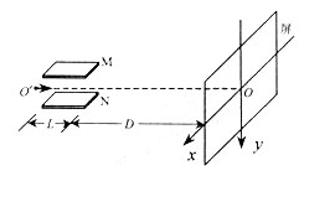
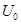,且N板电势比M板高，电子飞出平行板时的动能多大？
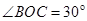。可视为质点的小滑块从轨道AB上高H处的某点由静止滑下，用力传感器测出滑块经过圆轨道最高点D时对轨道的压力为F，并得到如图乙所示的压力F与高度H的关系图象，取
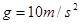。求：
=6.5R，板右端到C的距离L在R＜L＜5R范围内取值，E距A为S=5R，物块与传送带、物块与滑板间的动摩擦因数均μ=0.5，重力加速度取g。
