Question

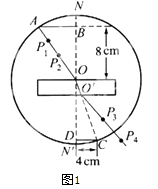
【题目】如图所示，质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点，水平轻质弹簧一端栓在固定挡板P上，另一端与靶盒A连接．Q处有一固定的发射器B，它可以瞄准靶盒发射一颗水平速度为v0=50m/s，质量m=0.010kg的弹丸，当弹丸打入靶盒A后，便留在盒内，碰撞时间极短．不计空气阻力．求：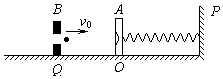

（1）弹丸进入靶盒A后，弹丸与靶盒A的共同速度设为v；
（2）弹丸进入靶盒A后，弹簧的最大弹性势能为多少？

Answer 1

【答案】
（1）解：弹丸进入靶盒A后，弹丸与靶盒A的共同速度设为v，选取向右为正方向，由弹丸与靶盒A组成的系统动量守恒得：

mv0=（m+M）v

所以：v= = =10m/s．

答：弹丸进入靶盒A后，弹丸与靶盒A的共同速度v为10m/s；

（2）解：当靶盒A的速度减为零时，弹簧的弹性势能最大，由系统机械能守恒得弹簧的最大弹性势能为：

Ep= （m+M）v2= J=2.5J

答：弹丸进入靶盒A后，弹簧的最大弹性势能为2.5J．

【解析】（1）弹丸打入靶盒A的过程，由于碰撞时间极短，弹丸与靶盒A组成的系统动量守恒，根据动量守恒定律列出等式，求出碰撞后的共同速度v；（2）弹丸进入靶盒A后压缩弹簧，弹簧的最大弹性势能等于碰撞后瞬间系统的动能，由系统机械能守恒求出弹簧的最大弹性势能．
【考点精析】认真审题，首先需要了解机械能守恒及其条件(在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变)，还要掌握机械能综合应用(系统初态的总机械能E 1 等于末态的总机械能E 2 ，即E1 =E2；系统减少的总重力势能ΔE P减 等于系统增加的总动能ΔE K增 ，即ΔE P减 =ΔE K增；若系统只有A、