题目内容
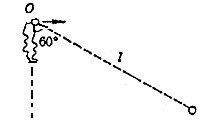
长为L的轻绳一端系于固定点O,另一端系质量为m的小球.将小球从O点正下方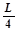 处,以一定初速度水平向右抛出,经一定时间绳被拉直以后,小球将以O为支点在竖直平面内摆动。已知绳刚被拉直时,绳与竖直线成60°角,如右图所示,
处,以一定初速度水平向右抛出,经一定时间绳被拉直以后,小球将以O为支点在竖直平面内摆动。已知绳刚被拉直时,绳与竖直线成60°角,如右图所示,
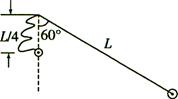
⑴求:小球水平抛出时的初速度v0
⑵在绳被拉紧的瞬间,小球立即做圆周运动;求小球摆到最低点时,绳所受拉力T.
【答案】
⑴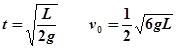 ⑵
⑵
【解析】⑴轻绳伸直前小球做平抛运动,设小球平抛运动的时间为t,则
 ①
①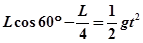 ② 联立①②解得
② 联立①②解得 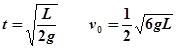
⑵绳伸直瞬间小球速度的水平分量如 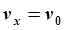 , 竖直分量
, 竖直分量 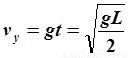 ,则小球速度大小
,则小球速度大小 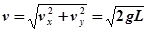 ,设此时小球速度与竖直方向夹角为θ,则
,设此时小球速度与竖直方向夹角为θ,则 ,所以 θ=60° 这说明绳刚伸直瞬间小球的初速度恰好沿绳方向,绳拉直后,小球的速度变为0,接着小球向下摆动,由机械能守恒定律可得小球在最低点的动能:
,所以 θ=60° 这说明绳刚伸直瞬间小球的初速度恰好沿绳方向,绳拉直后,小球的速度变为0,接着小球向下摆动,由机械能守恒定律可得小球在最低点的动能:
 在最低点用向心力公式得
在最低点用向心力公式得 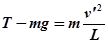 ④
④
联立③、④两式解得 
本题考查平跑运动规律的应用,绳子伸直前小球做平抛运动,由位移为绳子的长度,竖直方向自由落体运动的位移公式和水平方向的匀速直线运动公式列公式可得第一问,在第二问中根据第一问的运动时间可以求出绳子伸直的水平和竖直分速度,可求得和速度方向及大小,在绳子绷紧瞬间沿绳子方向的分速度减小到零,随后小球做单摆运动,到最低点由圆周运动和机械能守恒定律求解

练习册系列答案
相关题目
 长为L的轻绳一端系于固定点O,另一端系质量为m的小球.将小球从O点正下方
长为L的轻绳一端系于固定点O,另一端系质量为m的小球.将小球从O点正下方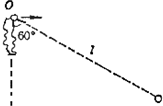 如图,长为L的轻绳一端系于固定点O,另一端系质量为m的小球.将小球从O点以一定初速水平向右抛出,经一定时间绳被拉直,以后小球将以O为支点在竖直平面内摆动.已知绳刚被拉直时,绳与竖直线成60度角,求:
如图,长为L的轻绳一端系于固定点O,另一端系质量为m的小球.将小球从O点以一定初速水平向右抛出,经一定时间绳被拉直,以后小球将以O为支点在竖直平面内摆动.已知绳刚被拉直时,绳与竖直线成60度角,求: (2006?淮北模拟)如图所示,长为L的轻绳一端系于固定点O,另一端系质量为m的小球,将小球从O点正下方
(2006?淮北模拟)如图所示,长为L的轻绳一端系于固定点O,另一端系质量为m的小球,将小球从O点正下方