题目内容
质量为m、带电量为+q的小金属块A以初速度v0从光滑水平高台上飞出．已知在高台边缘的右面空间中存在水平向左的匀强电场，场强大小E=| 2mg |
| q |
分析：小金属块水平方向向右做匀减速直线运动，竖直方向做自由落体运动；
对水平分运动，根据速度位移公式求解距高台边缘的最大水平距离；
求解出水平分速度和竖直分速度合速度，运用数学知识求解最小值．
对水平分运动，根据速度位移公式求解距高台边缘的最大水平距离；
求解出水平分速度和竖直分速度合速度，运用数学知识求解最小值．
解答：解：A、电场力F=qE=q?
=2mg，向左，故小金属块水平方向向右做匀减速直线运动，竖直方向做自由落体运动，合运动不是平抛运动，故A错误；
B、小金属块水平方向先向右做匀减速直线运动，然后向左做匀加速直线运动，故一定会与高台边缘相碰，故B正确；
C、小金属块水平方向先向右做匀减速直线运动，加速度为-2g，根据速度位移关系公式，有：xm=
=
，故C正确；
D、小金属块水平方向向右做匀减速直线运动，分速度vx=v0-gt；
竖直方向做自由落体运动，分速度vy=gt；
合速度v=
=
=
，根据二次函数知识，当t=
=
时，有极小值
，故D正确；
故选BCD．
| 2mg |
| q |
B、小金属块水平方向先向右做匀减速直线运动，然后向左做匀加速直线运动，故一定会与高台边缘相碰，故B正确；
C、小金属块水平方向先向右做匀减速直线运动，加速度为-2g，根据速度位移关系公式，有：xm=
| ||
| 2×2g |
| ||
| 4g |
D、小金属块水平方向向右做匀减速直线运动，分速度vx=v0-gt；
竖直方向做自由落体运动，分速度vy=gt；
合速度v=
|
| (v0-gt)2+(gt)2 |
2g2t2-2v0gt+
|
| 2v0g |
| 2×g2 |
| v0 |
| g |
| ||
| 5 |
故选BCD．
点评：本题关键将小金属块的运动沿着水平和竖直方向正交分解，然后根据分运动的位移公式和速度公式列式求解；对于D选项，要求解出合速度的表达式，根据二次函数的知识求解极值．
练习册系列答案
相关题目
真空中存在竖直向上的匀强电场和水平方向的匀强磁场，一质量为m，带电量为q的物体以速度v在竖直平面内做半径为R的匀速圆周运动，假设t=0时刻物体在轨迹最低点且重力势能为零，电势能也为零，那么，下列说法正确的是（ ）
如图所示，空中有水平向右的匀强电场和垂直于纸面向外的匀强磁场，质量为m，带电量为+q的滑块沿水平向右做匀速直线运动，滑块和水平面间的动摩擦因数为μ，滑块与墙碰撞后速度为原来的一半．滑块返回时，去掉了电场，恰好也做匀速直线运动，求原来电场强度的大小．
如图所示，绝缘光滑的半圆轨道位于竖直平面，竖直向下的匀强电场E穿过其中，在轨道的上缘有一个质量为m，带电量为+q的小球，由静止开始由半圆形轨道的顶点沿轨道运动，下列说法正确的是（ ）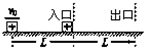
如图所示，在宽度为L的两虚线区域内存在匀强电场，一质量为m，带电量为+q的滑块（可看成点电荷），从距该区域为L的绝缘水平面上以初速度v0向右运动并进入电场区域，滑块与水平面间的动摩擦因数为μ．