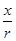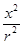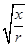题目内容
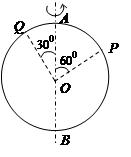
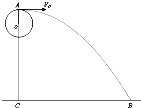
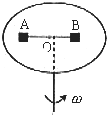
如图所示,某人站在一平台上,用长L=0.5m的轻细线拴一个质量为10kg的小球,让它在竖直平面内以O点为圆心做圆周运动,当小球转与最高点A时,人突然撒手.经0.8S小球落地,落地时小球速度方向与水平面成53°,(g=10m/s2)求:
(1)A点距地面高度;
(2)小球离开最高点时的速度;
(3)在不改变其他条件的情况下,要使小球从A处抛出落至B时的位移最小,人突然撒手时小球的速度为多少.
(1)A点距地面高度;
(2)小球离开最高点时的速度;
(3)在不改变其他条件的情况下,要使小球从A处抛出落至B时的位移最小,人突然撒手时小球的速度为多少.

(1)人突然撒手后小球做平抛运动,则A点距地面高度为:
h=
gt2=
×10×0.82m=3.2m ①
(2)设小球离开最高点时的速度为v0
则落地速度为:v=
②
从最高点到落地点,有动能定理得:
mgh=
mv2-
mv02 ③
①②③联立得:
小球离开最高点时的速度为:v0=6m/s
(3)在不改变其他条件的情况下,要使小球从A处抛出落至B时的位移最小即初速度最小,
即在最高点只有重力提供向心力,根据牛顿第二定律得:
mg=m
vmin=
=
m/s=
m/s
答:(1)A点距地面高度为3.2m;
(2)小球离开最高点时的速度为6m/s;
(3)人突然撒手时小球的速度为
m/s.
h=
| 1 |
| 2 |
| 1 |
| 2 |
(2)设小球离开最高点时的速度为v0
则落地速度为:v=
| v0 |
| cos53° |
从最高点到落地点,有动能定理得:
mgh=
| 1 |
| 2 |
| 1 |
| 2 |
①②③联立得:
小球离开最高点时的速度为:v0=6m/s
(3)在不改变其他条件的情况下,要使小球从A处抛出落至B时的位移最小即初速度最小,
即在最高点只有重力提供向心力,根据牛顿第二定律得:
mg=m
| vmin2 |
| L |
vmin=
| gL |
| 10×0.5 |
| 5 |
答:(1)A点距地面高度为3.2m;
(2)小球离开最高点时的速度为6m/s;
(3)人突然撒手时小球的速度为
| 5 |

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
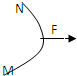
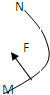
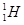 )和α粒子(
)和α粒子(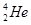 )以相同的初速度垂直进入同一匀强磁场做匀速圆周运动.则质子和α粒子的轨道半径之比为
)以相同的初速度垂直进入同一匀强磁场做匀速圆周运动.则质子和α粒子的轨道半径之比为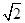 ∶1
∶1