Question

【题目】如图所示，AB、AC两光滑细杆组成的直角支架固定在竖直平面内，AB与水平面的夹角为30°，两细杆上分别套有带孔的a、b两小球，在细线作用下处于静止状态，细线恰好水平．某时刻剪断细线，当两球均下滑到支架底端时，两球( )

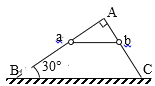
A. 下滑的时间相等

B. 下滑过程中重力做功相等

C. 到底端时的速率相等

D. 到底端时的动能相等

Answer 1

【答案】C

【解析】

根据牛顿第二定律和位移公式结合计算下滑的时间．根据平衡条件比较质量的大小，即可得出重力做功的大小．由机械能守恒定律分析到底端时的速率和动能大小；

A、设两球下滑的高度为h，对a球有：，，得；同理：对b有：，，得，则，故A错误；

B、根据平衡条件：，，故，则有，，所以，故B错误；

C、对于任意一球，由机械能守恒定律可知：，解得：，故有，故C正确；

D、到底端时的速率相等，而，所以到底端时的动能：，故D错误；

故选C。