题目内容
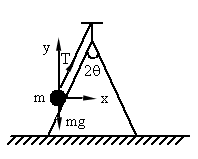
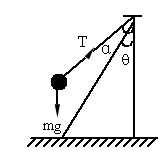
如图所示,顶角为2q 的光滑圆锥面,在顶尖上拴有一摆长为l的摆,摆球质量为m,当摆球以w 的角速度在水平面内做匀速圆周运动时,摆线上的张力多大?

答案:略
解析:
解析:
|
摆球刚好不离开锥面的临界状态是摆球虽然与锥面接触,但与锥面无相互作用的弹力,对摆球受力分析,建立坐标系如图所示,设此时小球的角速度为  ,根据牛顿运动定律有 ,根据牛顿运动定律有
联立两式解得 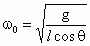 . .
讨论: (1)当 时,摆球受力如图,得 时,摆球受力如图,得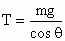 . .
T (2) 当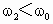 时,锥面对球有支持力,摆球受力情况如图所示,列方程有 时,锥面对球有支持力,摆球受力情况如图所示,列方程有
联立③④两式解得
(3) 当 时,摆球离开锥面,设摆线与竖直方向的夹角为a,受力情况如图所示,得 时,摆球离开锥面,设摆线与竖直方向的夹角为a,受力情况如图所示,得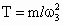 . .
由于题中w未给出确定数值,因此当摆球的角速度较小时,球贴着锥面运动;当摆球的角速度较大时,球会离开锥面做匀速圆周运动.所以应首先分析摆球的临界状态,然后再分情况对球作受力分析,应用牛顿运动定律进行求解. 此题常见的一种错误解法是只分析摆球在锥面上的运动情况,得出上述讨论 (2)的结论,而忽略了上述(1)(3)两种情况,没有对物体的运动进行全面分析是导致漏解的原因.本题重点考查对物体运动情况全面分析的能力和临界状态的分析,分析此类问题的方法一般是采用假设法或极限思维.如本题中,假设摆球的角速度较小,球的运动情况怎样和假设摆球的角速度较大时,摆球的运动情况又会怎样,即可得知存在的临界情况,这是一个难点,应注意练习掌握. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
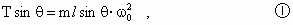

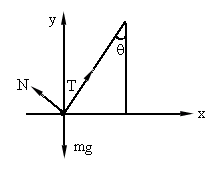


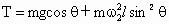
 如图所示,顶角为2θ、内壁光滑的圆锥体倒立竖直固定在P点,中心轴PO位于竖直方向,一质量为m的质点以角速度ω绕竖直轴沿圆锥内壁在同一水平面上做匀速圆周运动,已知a、b两点为质点m运动所通过的圆周一直径上的两点,求质点m从a点经半周运动到b点时,圆锥体内壁对质点施加的弹力冲量.
如图所示,顶角为2θ、内壁光滑的圆锥体倒立竖直固定在P点,中心轴PO位于竖直方向,一质量为m的质点以角速度ω绕竖直轴沿圆锥内壁在同一水平面上做匀速圆周运动,已知a、b两点为质点m运动所通过的圆周一直径上的两点,求质点m从a点经半周运动到b点时,圆锥体内壁对质点施加的弹力冲量.

