��Ŀ����
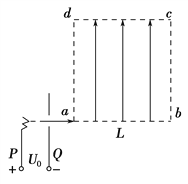
����Ŀ����ͼ��ʾ���뾶R=0.2m�Ĺ⻬�ķ�֮һԲ���MN��ֱ�̶����ã�ĩ��N��һ��L=0.8m��ˮƽ���ʹ�ƽ�����У�ˮƽ�νӲ�����е����ʧ�������ֵİ뾶��С�����ʹ��Ժ㶨���ٶ���0��˳ʱ���˶������ʹ��ϱ��������ĸ߶�h=1.25m�����Ҳ��������һֱ��D=0.5m��Բ�ζ�����������˵�A���봫�ʹ��Ҷ˵�ˮƽ����x=1m��B���ڶ��ڵ����Ҷˣ���ʹ����Ϊm=0.5kg��С����M���ɾ�ֹ��ʼ�ͷţ��������ʹ�����ƽ���˶���С������Ϊ�ʵ㣬���ƿ������������ʹ���С���֮��Ķ�Ħ��������=0.5��gȡ10m/s2����

��1����v0=3m/s����С����ڴ��ʹ�����Ħ�����������ܣ�
��2����ҪʹС��������붴�У����ʹ����ٶ���0Ӧ���������
���𰸡���1��0.25J ��2��2m/s��v0��3m/s��
��������
��1����С������N����ٶ�ΪvN����M��N��е���غ㣬�ɻ�е���غ㶨�ɵã�
mgR=![]() mvN2��
mvN2��
��ã�vN=2m/s��
�����ʹ�v0=3m/s����С������Ҫ�����˶�����С�����У�
��mg=ma��
��ã�a=5m/s2
��2m/s��3m/s������λ�ƣ�
x=![]() =0.5m��0.8m��
=0.5m��0.8m��
ʱ�䣺
t=![]() =0.2s
=0.2s
֮����Ծ�ֹ��
�ڻ����˶�0.5m���ʱ���ڣ����ʹ�λ�ƣ�
x=v0t=0.6m
����
��x=0.6m��0.5m=0.1m
���ܣ�
Q=��mg��x=0.25J��
��2����ƽ���˶����ɣ��У�
![]()
�����t=0.5s
��С����պô�A����붴����Ҫ����ٶ�
v1=![]() =2m/s
=2m/s
��С����պô�B����붴����Ҫ����ٶ�
v2=![]() =3m/s
=3m/s
����Ҫ���붴�У����ʹ��ٶ�Ӧ�����������
2m/s��v0��3m/s��