题目内容
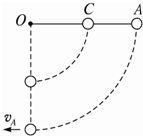 一根长为L、质量不计的硬杆OA,杆的中点C及A端各固定一个质量均为m的小球,杆、球系统可在竖直平面内绕O端的水平轴转动,如图所示.若开始时杆处于水平位置,并由静止释放,当该系统在转动过程中通过竖直位置时,A端小球的速度va为多大?,中点小球的机械能比在水平位置时减少了多少?
一根长为L、质量不计的硬杆OA,杆的中点C及A端各固定一个质量均为m的小球,杆、球系统可在竖直平面内绕O端的水平轴转动,如图所示.若开始时杆处于水平位置,并由静止释放,当该系统在转动过程中通过竖直位置时,A端小球的速度va为多大?,中点小球的机械能比在水平位置时减少了多少?分析:小球A、C系统中,只有重力势能和动能相互转化,机械能守恒,根据机械能守恒定律列式求解.
解答:解:在转动过程中,A、C两球的角速度相同,设A球的速度为vA,C球的速度为vC,则有
vA=2vC ①
以A、C和杆组成的系统机械能守恒,由机械能守恒定律,并选最低点为零势能参考平面,则有
E1=mg?L+mg?L=2mgL,
E2=mg
+
m
+
m
E1=E2
即2mgL=mg
+
+
②
①②两式结合可以求出
vA=
VC=
小球C的机械能减少量为
E=mg?L-(mg
+
)=
mgL.
故A端小球的速度va为
,中点小球的机械能比在水平位置时减少了
mgL.
vA=2vC ①
以A、C和杆组成的系统机械能守恒,由机械能守恒定律,并选最低点为零势能参考平面,则有
E1=mg?L+mg?L=2mgL,
E2=mg
| L |
| 2 |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 C |
E1=E2
即2mgL=mg
| L |
| 2 |
| L |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 C |
①②两式结合可以求出
vA=
|
VC=
|
小球C的机械能减少量为
E=mg?L-(mg
| L |
| 2 |
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 5 |
故A端小球的速度va为
|
| 1 |
| 5 |
点评:本题关键是系统内部只有重力势能和动能相互转化,机械能守恒;判断机械能是否守恒可以看是否只有重力做功,也可以看是否只有重力势能和动能相互转化.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
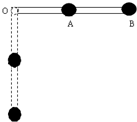 如图所示,一根长为L,质量不计的硬杆,在中点及右端各固定一个质量为m的小球,杆可带动小球在竖直平面内绕O点转动.若开始时杆处于水平位置,由静止开始释放,当杆下落到竖直位置时,下列说法中正确的是( )
如图所示,一根长为L,质量不计的硬杆,在中点及右端各固定一个质量为m的小球,杆可带动小球在竖直平面内绕O点转动.若开始时杆处于水平位置,由静止开始释放,当杆下落到竖直位置时,下列说法中正确的是( )A、B球的速率为
| ||||
B、B球的机械能减少了
| ||||
C、A球的机械能减少了
| ||||
| D、每个小球的机械能都不变 |
 在一根长为L、质量不计的细杆中点和末端各连一质量为m的小球B和C,如图所示,杆可以在竖直平面内绕固定点A转动,将杆拉到某位置放开,末端C球摆到最低位置时,杆BC段受到的拉力刚好等于C球重力的2倍.(g=10m/s2)求:
在一根长为L、质量不计的细杆中点和末端各连一质量为m的小球B和C,如图所示,杆可以在竖直平面内绕固定点A转动,将杆拉到某位置放开,末端C球摆到最低位置时,杆BC段受到的拉力刚好等于C球重力的2倍.(g=10m/s2)求: