题目内容
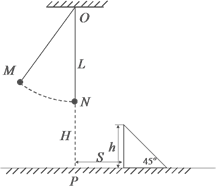
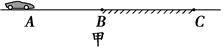
（12分）如图所示，在粗糙水平台阶上放置一质量m=0.5kg的小物块，它与水平台阶间的动摩擦因数μ=0.5，与台阶边缘O点的距离s=5m。在台阶右侧固定一个1/4圆弧挡板，圆弧半径R=1m，圆弧的圆心也在O点。今以O点为原点建立平面直角坐标系xOy。现用F=5N的水平恒力拉动小物块，一段时间后撤去拉力，小物块最终水平抛出并击中挡板。（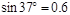
，取g=10m/s2）
（1）若小物块恰能击中挡板上的P点（OP与水平方向夹角为37°），求其离开O点时的速度大小；
（2）为使小物块击中挡板，求拉力F作用的最短时间。
（1）
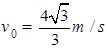（2）1s.
解析试题分析：（1）小物块从O到P做平抛运动：水平方向：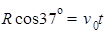
；竖直方向：
；解得
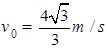
（2）为使小物块击中档板，小物块必须能运动到O点。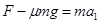
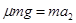
所以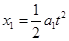 
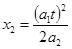
则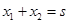 
解得：最短作用时间为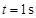
（用动能定理求解也相应给分）
考点：平抛运动及牛顿定律的应用。
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
、
；
、
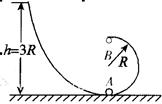
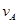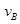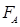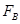大小；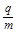
＝1.0×108C/kg，初速度v0＝2×105m/s（粒子重力不计），在A、B两板间加上如图乙所示的电压，电压的周期T＝2.0×10－6s，t＝0时刻A板电势高于B板电势，两板间电场可视为匀强电场，电势差U0＝360V，A、B板右侧相距s＝2cm处有一边界MN，在边界右侧存在一垂直纸面向里的匀强磁场，磁感应强度B＝
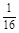T，磁场中放置一“＞”型荧光板，位置如图所示，板与水平方向夹角θ＝37°，不考虑粒子之间相互作用及粒子二次进入磁场的可能，求：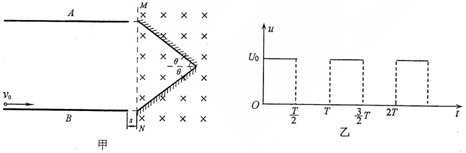
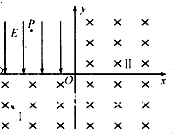
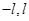）点由静止释放，沿垂直于x轴的方向进入磁场I，接着以垂直于y轴的方向进入磁场Ⅱ，不计粒子重力．
