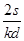题目内容
如图,在一个平面直角坐标系内,原点O处有一质点,质量为m。为使质点到达坐标为(d,d)的点P,现给质点施以大小为F的恒力,在起初的时间t1内该力方向为x轴正方向,之后的时间t2内该力变为y轴正方向,经过这两段运动质点刚好到达P点。试求:

(1)比值t1:t2;
(2)质点到达P点时的速度。

(1)比值t1:t2;
(2)质点到达P点时的速度。
(1) (2)v2=
(2)v2=
 (2)v2=
(2)v2=
(1)物体运动时的加速度
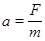 (1)
(1)
在t1时间内x方向做匀变速直线运动,位移
x1= (2)
(2)
t1时间末速度
v1=at1 (3)
t2时间内x方向为匀速直线运动,位移
x2=v1t2=at1t2 (4)
y方向做匀变速直线运动,位移
 (5)
(5)
y方向末速度
v2=at2 (6)
物体最终到达P点,有
x1+x2=d (7)
y2=d (8)
根据(2)(4)(5)(7)(8)解得
 (9)
(9)
(2)根据(1)(5)(8)可解得:
t2= (10)
(10)
由(9)(10)可得
t1=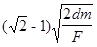 (11)
(11)
由(1)(3)(11)可得质点x方向末速度为
v1= (12)
(12)
由(1)(6)(10)可得质点y方向末速度为
v2= (13)
(13)
评分标准:
(1)问6分,(2)(4)(5)(7)(8)(9)各1分
(2)问4分,(10)(11)(12)(13)各1分,末速度表达为大小和方向也可。
本题考查运动的合成与分解,当拉力F沿x轴方向时,物体沿着x轴做匀加速直线运动,先由牛顿第二定律求得加速度,再由运动学公式求得在t1时刻的速度大小和位移大小,当拉力F沿y轴方向时,物体做类平抛运动,在x轴方向匀速运动,沿y轴方向做匀加速直线运动,经过t2时间由v=at求得y轴方向分速度,再由运动学公式求得y轴方向位移,由P点坐标可知x轴和y轴方向位移均为d,列出公式可求得运动时间比值
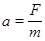 (1)
(1)在t1时间内x方向做匀变速直线运动,位移
x1=
 (2)
(2)t1时间末速度
v1=at1 (3)
t2时间内x方向为匀速直线运动,位移
x2=v1t2=at1t2 (4)
y方向做匀变速直线运动,位移
 (5)
(5)y方向末速度
v2=at2 (6)
物体最终到达P点,有
x1+x2=d (7)
y2=d (8)
根据(2)(4)(5)(7)(8)解得
 (9)
(9)(2)根据(1)(5)(8)可解得:
t2=
 (10)
(10)由(9)(10)可得
t1=
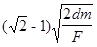 (11)
(11)由(1)(3)(11)可得质点x方向末速度为
v1=
 (12)
(12)由(1)(6)(10)可得质点y方向末速度为
v2=
 (13)
(13)评分标准:
(1)问6分,(2)(4)(5)(7)(8)(9)各1分
(2)问4分,(10)(11)(12)(13)各1分,末速度表达为大小和方向也可。
本题考查运动的合成与分解,当拉力F沿x轴方向时,物体沿着x轴做匀加速直线运动,先由牛顿第二定律求得加速度,再由运动学公式求得在t1时刻的速度大小和位移大小,当拉力F沿y轴方向时,物体做类平抛运动,在x轴方向匀速运动,沿y轴方向做匀加速直线运动,经过t2时间由v=at求得y轴方向分速度,再由运动学公式求得y轴方向位移,由P点坐标可知x轴和y轴方向位移均为d,列出公式可求得运动时间比值

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 匀速转动,∠ABC为直角且AB=BC=L.一质点P沿AD边作匀速运动,当三角形板ACD转动一周时P恰好从A点运动到B点,关于质点P下列说法正确的是 ( )
匀速转动,∠ABC为直角且AB=BC=L.一质点P沿AD边作匀速运动,当三角形板ACD转动一周时P恰好从A点运动到B点,关于质点P下列说法正确的是 ( )

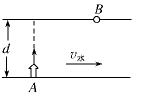
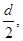 k为常量),要使小船能够到达距离A正对岸为s的B码头,则( )
k为常量),要使小船能够到达距离A正对岸为s的B码头,则( )