题目内容
5. 如图所示,MN、PQ是与水平面成θ角的两条平行光滑且足够长的金属导轨,其电阻忽略不计.空间存在着垂直于轨道平面向上的匀强磁场,磁感应强度大小为B.导体棒ab、cd垂直于导轨放置,且与轨道接触良好,每根导体棒的质量均为m,电阻均为r,轨道宽度为L.与导轨平行的绝缘细线一端固定,另一端与ab棒中点连接,细线承受的最大拉力Tm=2mgsinθ.今将cd棒由静止释放,则细线被拉断时,cd棒的( )
如图所示,MN、PQ是与水平面成θ角的两条平行光滑且足够长的金属导轨,其电阻忽略不计.空间存在着垂直于轨道平面向上的匀强磁场,磁感应强度大小为B.导体棒ab、cd垂直于导轨放置,且与轨道接触良好,每根导体棒的质量均为m,电阻均为r,轨道宽度为L.与导轨平行的绝缘细线一端固定,另一端与ab棒中点连接,细线承受的最大拉力Tm=2mgsinθ.今将cd棒由静止释放,则细线被拉断时,cd棒的( )| A. | 速度大小是$\frac{2mgrsinθ}{{B}^{2}{L}^{2}}$ | B. | 速度大小是$\frac{mgrsinθ}{{B}^{2}{L}^{2}}$ | ||
| C. | 加速度大小是2gsinθ | D. | 加速度大小是0 |
分析 细线被拉断时,拉力达到最大值Tm=2mgsinθ.根据平衡条件和安培力的表达式,求出此时cd棒的速度大小.根据牛顿第二定律求解加速度的大小.
解答 解:AB、据题知,细线被拉断时,拉力达到Tm=2mgsinθ.
根据平衡条件得:对ab棒:Tm=F安+mgsinθ.则得ab棒所受的安培力大小为F安=mgsinθ;
由于两棒的电流相等,所受的安培力大小相等.
由E=BLv、I=$\frac{E}{2r}$,F安=BIL,则得F安=$\frac{{B}^{2}{L}^{2}v}{2r}$
联立解得,cd棒的速度为 v=$\frac{2mgrsinθ}{{B}^{2}{L}^{2}}$.故A正确,B错误.
CD、对cd棒:根据牛顿第二定律得:mgsinθ-F安=ma,代入得a=0,故C错误,D正确.
故选:AD
点评 本题实质上电磁感应中平衡问题,关键要会推导安培力与速度的关系式,运用力学的基本知识解答.

练习册系列答案
相关题目
15.关于磁感线,下列说法中正确的是( )
| A. | 磁感线是实际存在于磁场中的线 | |
| B. | 磁感线上任意一点的切线方向,都跟该点的磁场方向一致 | |
| C. | 磁感线有可能出现相交的情况 | |
| D. | 磁场中的小磁针静止时北极所指的方向就是该点的磁场方向 |
13.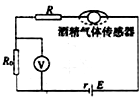 酒精测试仪利用的是一种二氧化锡半导体型酒精气体传感器,酒精气体传感器的电阻随酒精气体浓度的变化而变化,在如图所示的电路中,R和R0为定值电阻,不同的酒精气体浓度对应着传感器的不同电阻,因此,显示仪表读数的指针与酒精气体浓度有了对应关系,如果二氧化锡半导体型酒精气体传感器电阻 r′的倒数与酒精气体的浓度成正比,那么,电压表示数U与酒精气体浓度c之间的对应关系正确的是( )
酒精测试仪利用的是一种二氧化锡半导体型酒精气体传感器,酒精气体传感器的电阻随酒精气体浓度的变化而变化,在如图所示的电路中,R和R0为定值电阻,不同的酒精气体浓度对应着传感器的不同电阻,因此,显示仪表读数的指针与酒精气体浓度有了对应关系,如果二氧化锡半导体型酒精气体传感器电阻 r′的倒数与酒精气体的浓度成正比,那么,电压表示数U与酒精气体浓度c之间的对应关系正确的是( )
 酒精测试仪利用的是一种二氧化锡半导体型酒精气体传感器,酒精气体传感器的电阻随酒精气体浓度的变化而变化,在如图所示的电路中,R和R0为定值电阻,不同的酒精气体浓度对应着传感器的不同电阻,因此,显示仪表读数的指针与酒精气体浓度有了对应关系,如果二氧化锡半导体型酒精气体传感器电阻 r′的倒数与酒精气体的浓度成正比,那么,电压表示数U与酒精气体浓度c之间的对应关系正确的是( )
酒精测试仪利用的是一种二氧化锡半导体型酒精气体传感器,酒精气体传感器的电阻随酒精气体浓度的变化而变化,在如图所示的电路中,R和R0为定值电阻,不同的酒精气体浓度对应着传感器的不同电阻,因此,显示仪表读数的指针与酒精气体浓度有了对应关系,如果二氧化锡半导体型酒精气体传感器电阻 r′的倒数与酒精气体的浓度成正比,那么,电压表示数U与酒精气体浓度c之间的对应关系正确的是( )| A. | U越大,表示r′越大,c越大,c与U成正比 | |
| B. | U越小,表示r′越小,c越大,但是c与U成正比 | |
| C. | U越小,表示c越小,c与U成反比 | |
| D. | U越大,表示c越大,但是c与U不成正比 |
20.下列说法中正确的是( )
| A. | 激光比普通光源的相干性好 | |
| B. | 紫光在水中的传播速度大于红光在水中的传播速度 | |
| C. | 在光的衍射实验中,出现明条纹的地方光子到达的概率较大 | |
| D. | 氘和氦3的核聚变反应方程式:${\;}_{1}^{2}$H+${\;}_{2}^{3}$He→${\;}_{2}^{4}$He+X,其中X是正电子 |
10.某同学在做探究弹力和弹簧伸长的关系的实验中,设计了如图所示的实验装置.所用的钩码每只的质量都是30g,他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,将数据填在了下面的表中.(弹力始终未超过弹性限度,取g=9.8m/s2)
(1)根据这些实验数据在图作出弹簧所受弹力大小F跟弹簧总长L之间的函数关系图线.则图线与横坐标的交点表示表示弹簧的原长.
(2)从所得图线可知该弹簧的劲度k=25.9.
| 砝码质量(g) | 0 | 30 | 60 | 90 | 120 | 150 |
| 弹簧总长(cm) | 6.00 | 7.15 | 8.34 | 9.48 | 10.64 | 11.79 |
| 弹力大小(N) |
(2)从所得图线可知该弹簧的劲度k=25.9.
15.自然界中的两种电荷是( )
| A. | 正电荷,负电荷 | B. | 正电荷,阴电荷 | C. | 阳电荷,负电荷 | D. | 阳电荷,阴电荷 |

 如图所示,带电平行金属板相距为2R,在两板间半径为R的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度为B,两板及其左侧边缘连线均与磁场边界刚好相切.一质子(不计重力)沿两板间中心线O1O2从左侧O1点以某一速度射入,沿直线通过圆形磁场区域,然后恰好从极板边缘飞出,在极板间运动时间为t0.若仅撤去磁场,质子仍从O1点以相同速度射入,经$\frac{{t}_{0}}{2}$时间打到极板上.
如图所示,带电平行金属板相距为2R,在两板间半径为R的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度为B,两板及其左侧边缘连线均与磁场边界刚好相切.一质子(不计重力)沿两板间中心线O1O2从左侧O1点以某一速度射入,沿直线通过圆形磁场区域,然后恰好从极板边缘飞出,在极板间运动时间为t0.若仅撤去磁场,质子仍从O1点以相同速度射入,经$\frac{{t}_{0}}{2}$时间打到极板上. 如图所示,在水平路上骑摩托车的人,遇到一个壕沟,沟两岸高低差0.8m,水平间距5m,摩托车要安全越过这个壕沟,过壕沟时的初速度至少多大.空气阻力忽略不计.
如图所示,在水平路上骑摩托车的人,遇到一个壕沟,沟两岸高低差0.8m,水平间距5m,摩托车要安全越过这个壕沟,过壕沟时的初速度至少多大.空气阻力忽略不计.