题目内容
【题目】如图所示,两轮通过边缘接触,形成摩擦传动装置,设接触处不打滑.已知大轮B的半径是小轮A半径的2倍,设主动轮A转动时其边缘的角速度为ω,线速度为v,求: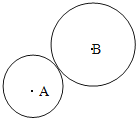
(1)A、B两轮的转动周期之比
(2)B轮边缘上一点的线速度
(3)B轮转动的角速度.
【答案】
(1)
根据 ![]() 知,线速度相等,A、B两轮的半径比为1:2,则角速度之比为2:1.A轮的角速度为ω,则B轮的角速度为0.5ω.根据
知,线速度相等,A、B两轮的半径比为1:2,则角速度之比为2:1.A轮的角速度为ω,则B轮的角速度为0.5ω.根据 ![]() 知,则周期比1:2.
知,则周期比1:2.
(2)
A、B边缘具有相同的线速度,所以B轮的线速度大小为v.
(3)
B轮转动的角速度0.5ω
【解析】根据 ![]() 知,线速度相等,A、B两轮的半径比为1:2,则角速度之比为2:1.A轮的角速度为ω,则B轮的角速度为0.5ω.根据
知,线速度相等,A、B两轮的半径比为1:2,则角速度之比为2:1.A轮的角速度为ω,则B轮的角速度为0.5ω.根据 ![]() 知,则周期比1:2.A、B边缘具有相同的线速度,所以B轮的线速度大小为v.
知,则周期比1:2.A、B边缘具有相同的线速度,所以B轮的线速度大小为v.
(1)根据 ![]() 求出A、B两轮的周期之比.(2)A、B摩擦转动,接触点无打滑现象,知A、B边缘具有相同的线速度.(3)根据
求出A、B两轮的周期之比.(2)A、B摩擦转动,接触点无打滑现象,知A、B边缘具有相同的线速度.(3)根据 ![]() 求出两轮子的角速度之比,从而求出A轮的角速度.
求出两轮子的角速度之比,从而求出A轮的角速度.

练习册系列答案
相关题目