题目内容
如图所示，一段曲线（抛物线）是某物体做平抛运动轨迹的一部分，将该曲线放在边长已知的方格坐标纸上，由此我们可以计算出（重力加速度g已知）
| A．物体抛出的初始速度 |
| B．物体任意时刻的动能和重力势能 |
| C．物体任意时刻的速度 |
| D．物体的抛出位置 |
ACD
解析试题分析：平抛运动水平分运动为匀速直线运动，设方格的边长为L，由坐标纸知，发生连续三段3L长的水平位移所用时间T相等，在这连续相等的时间T内，竖直分位移之比为1∶3∶5，则可知坐标纸上起始点的竖直分速度为0，可知物体抛出的位置即为坐标纸的超始点，D正确；由Δx=gT2 可求时间间隔T，由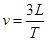
可求物体抛出时的初速度，A正确；平抛运动的竖直分运动为自由落体运动，可求任意时刻的竖直分速度，由平行四边形定则，可求任意时刻的速度，C正确；可求任意时刻的动能，但重力势能不可求，因为没有明确的参考平面，B错误。
考点：本题考查平抛运动规律。
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
如图所示，一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上．物体与斜面接触时速度与水平方向的夹角φ满足（ ）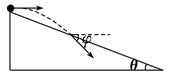
| A．tanφ＝sinθ | B．tanφ＝cosθ | C．tanφ＝tanθ | D．tanφ＝2tanθ |
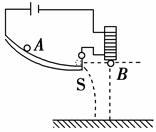
某人向放在水平地面的正前方小桶中水平抛球，结果球划着一条弧线飞到小桶的前方（如图所示）。不计空气阻力，为了能把小球抛进小桶中，则下次再水平抛时，他可能作出的调整为（ ）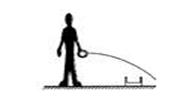
| A．增大初速度，抛出点高度变大 |
| B．增大初速度，抛出点高度不变 |
| C．初速度大小不变，降低抛出点高度 |
| D．初速度大小不变，提高抛出点高度 |
如图所示，在水平地面的A点以一定的速度v1与地面成θ角射出一弹丸，恰好垂直撞击到竖直壁上，欲使A点离竖直壁的水平距离最大，θ应该为（ ）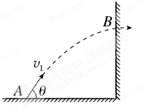
| A．0° | B．30° | C．45° | D．60° |
如图所示，x轴沿水平方向，y轴沿竖直方向，OM是与x轴成θ角的一条射线.现从坐标原点O以速度v0水平抛出一个小球，小球与射线OM交与P点，此时小球的速度v与OM的夹角为α，若保持方向不变而将小球初速度增大为2v0，小球与射线OM交与P'，此时小球的速度v与OM的夹角为α'，则（ ）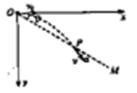
| A．小球从O运动到P'的时间是从O到P时间的2倍 |
| B．夹角α'是α的2倍 |
| C．小球通过P'点的速度为4v |
| D．OP'=4OP |
高处以初速度
水平抛出一物体，测得物体的水平射程为
。已知月球的半径为
，则月球的第一宇宙速度为（ ）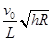
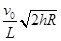
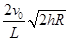
的速度水平抛出，在落地之前经过空中A、B两点．在A点小球速度方同与水平方同的夹角为
．在B点小球速度方同与水平方同的夹角为
（空气阻力忽略不计．g取
）．以下判断中正确的足
