题目内容
如图所示,水平面上固定有一个斜面,从斜面顶端向右平抛一只小球,当初速度为v0时,小球恰好落到斜面底端,小球的飞行时间为t0。现用不同的初速度v从该斜面顶端向右平抛这只小球,以下哪个图象能正确表示小球的飞行时间t随v变化的函数关系

C
解析试题分析:据题意,设斜面倾角为 ,小球做平抛运动,运动过程中水平位移为:
,小球做平抛运动,运动过程中水平位移为: ,竖直位移为:
,竖直位移为: ,由于斜面倾角不变,则有:
,由于斜面倾角不变,则有: ,整理得:
,整理得: ,当增加速度,时间与平抛速度成正比;小球落地后,由于高度不变,则小球的平抛运动时间不变;故选项C正确。
,当增加速度,时间与平抛速度成正比;小球落地后,由于高度不变,则小球的平抛运动时间不变;故选项C正确。
考点:本题考查平抛运动。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为了探究影响平抛运动水平射程的因素,某同学通过改变抛出点的高度及初速度的方法做了6次实验,实验数据记录如表.以下探究方案符合控制变量法的是
| 序号 | 抛出点的高度(m) | 水平初速度 (m/s) | 水平射程(m) |
| 1 | 0.20 | 2.0 | 0.40 |
| 2 | 0.20 | 3.0 | 0.60 |
| 3 | 0.45 | 2.0 | 0.60 |
| 4 | 0.45 | 4.0 | 1.20 |
| 5 | 0.80 | 2.0 | 0.80 |
| 6 | 0.80 | 6.0 | 2.40 |
B.若探究水平射程与高度的关系,可用表中序号为1、3、5的实验数据
C.若探究水平射程与高度的关系,可用表中序号为2、4、6的实验数据
D.若探究水平射程与初速度的关系,可用表中序号为2、4、6的实验数据
如图所示,一段曲线(抛物线)是某物体做平抛运动轨迹的一部分,将该曲线放在边长已知的方格坐标纸上,由此我们可以计算出(重力加速度g已知)
| A.物体抛出的初始速度 |
| B.物体任意时刻的动能和重力势能 |
| C.物体任意时刻的速度 |
| D.物体的抛出位置 |
如图所示,P、Q是高度不同的两点,P点比Q点高,从P、Q两点同时相向水平抛出两个小球,其运动轨迹相交于A点,则以下说法正确的是( )
| A. Q小球先落地 |
| B. P、Q两球在A点相遇 |
| C.从抛出到落地的整个过程中,P球的速度变化量比Q的速度变化量大 |
| D.从抛出到落地的整个过程中,两球的速度变化量相等 |
两相同高度的斜面,倾角分别为300、600,两小球分别由斜面顶端以相同水平速度v抛出,如图所示,假设两球能落在斜面上,则两球下落高度之比( )
| A.1:2 | B.3:1 | C.1:9 | D.9:1 |
如图所示,球网高出桌面H,网到桌边的距离为L。某人在乒乓球训练中,从左侧L/2处,将球沿垂直于网的方向水平击出,球恰好通过网的上沿落到右侧桌边缘。设乒乓球运动为平抛运动。则( )
| A.击球点的高度与网高度之比为2:1 |
| B.乒乓球在网左右两侧运动时间之比为2:1 |
| C.乒乓球过网时与落到桌边缘时速率之比为1:2 |
| D.乒乓球在左、右两侧运动速度变化量之比为1: 2 |

 B.vA<vB C.tA>tB D.
B.vA<vB C.tA>tB D.
 、
、 ,C落到水平面上时速度方向与水平方向的夹角为
,C落到水平面上时速度方向与水平方向的夹角为 ,则
,则
 B.
B.
 D.
D.
 ,一带正电的点电荷以初速度
,一带正电的点电荷以初速度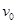 沿垂直电场方向从A点射入电场,一段时间后经过B点,此时其速度方向与电场方向的夹角为
沿垂直电场方向从A点射入电场,一段时间后经过B点,此时其速度方向与电场方向的夹角为 ,不计重力,则下列表达式正确的是
,不计重力,则下列表达式正确的是



